Целые решения неопределенных уравнений степени выше первой

Решение в целых числах неопределенных уравнений степени выше первой с целыми коэффициентами -во многих случаях задача более сложная, чем решение в целых числах неопределенных уравнений первой степени.

Индийские математики (V-XII вв.) нашли решение в целых числах некоторых уравнений второй степени с двумя неизвестными. С исчерпывающей полнотой задачу нахождения в целых числах неопределенных уравнений второй степени с двумя неизвестными решил в 1766 г. французский математик Ж. Лагранж.

Уравнения третьей степени с двумя неизвестными до сих пор до конца не исследованы. С некоторыми типами таких уравнений удалось справиться советскому математику Б. Н. Делоне. Заметим, что даже установить число решений таких уравнений третьей и более высоких степеней исключительно трудно.

В начале нашего столетия норвежский математик А. Туэ доказал интересную теорему: Неопределенное уравнение с целыми коэффициентами:

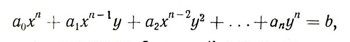
где п - целое число, большее 2, имеет только конечное множество решений (в частности, может не иметь решений) в целых числах, за исключением случаев, когда левая часть этого уравнения есть степень однородного двучлена первой степени или трехчлена второй степени.

Еще более трудным является вопрос о решении в целых числах неопределенных уравнений выше первой степени с тремя и более неизвестными. До сих пор неизвестен общий метод решения таких уравнений. Уравнение (1) является простейшим из них. Древние греки и даже вавилоняне знали тождество:

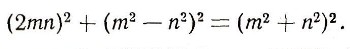
Пользуясь таким тождеством, нетрудно находить натуральные решения уравнения (1). Для этой цели нужно в формулах

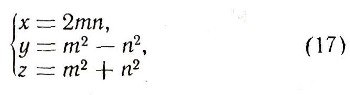
переменным т и п давать натуральные значения с условием, что m>n. При помощи простых соображений доказывается, что из формул (17) можно получить все решения уравнения (1) в натуральных и взаимно простых числах, если параметрам т и п давать натуральные, взаимно простые и разной четности значения с условием т>п.

Занимаясь неопределенными уравнениями, известный французский математик П. Ферма высказал в середине XVII в. предположение, что для любого натурального числа n, большего 2, уравнение

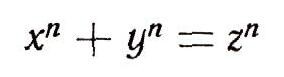
не имеет решений в натуральных числах. Для n=3 и n=4 это было доказано Л. Эйлером.

В дальнейшем предпринимались многочисленные попытки доказать это утверждение (так называемую великую теорему Ферма) полностью, но они не имели успеха. (В настоящее время теорема доказана для всех n<10000.)

Однако такие попытки не были безрезультатными, они содействовали возникновению и развитию нового отдела математики - алгебраической теории чисел.

В 1770 г. шотландский математик Э. Варинг высказал предположение, что для всякого натурального k, не равного 1, существует такое натуральное число г, что при любом натуральном N уравнение

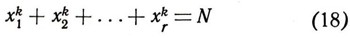
разрешимо в целых числах. Доказательство частного случая этого утверждения принадлежит французскому математику Ж. Лагранжу. Он установил, что всякое число можно представить в виде суммы четырех квадратов целых неотрицательных чисел, например :

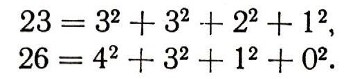
Полностью эту теорему доказал в 1909 г. немецкий математик Д. Гильберт. Но ему не удалось дать оценку минимального числа r, для которого уравнение (18) разрешимо в целых неотрицательных числах. Значительный успех в определении g (k) (так обозначают наименьшее r, для которого при любом натуральном N уравнение (18) разрешимо в целых неотрицательных числах) стал возможен только после создания советским математиком И. М. Виноградовым особого метода для решения этой и сходных с ней задач.

Любые достижения при решении неопределенных уравнений степени выше первой с тремя и более неизвестными обычно получаются с большим трудом. Это не случайно. Оказывается, не существует, общего метода - алгоритма, который бы позволил распознавать, разрешимо или нет в целых числах каждое из таких уравнений. Эту теорему удалось доказать в 1970 г. двадцатитрехлетнему ленинградскому математику Ю. В. Матиясевичу.

Сравнительно недавно стали изучаться показательные неопределенные уравнения. К этой области относится интересная теорема советского математика А. О. Гельфонда:

Уравнение а^x +b^y =с^z где a, b и с - целые, каждое из которых не равно ни нулю, ни, степени двойки, может иметь не более чем конечное число решений в целых числах х, у и z.

Наиболее трудны неопределенные уравнения, связанные каким-либо способом с простыми числами.

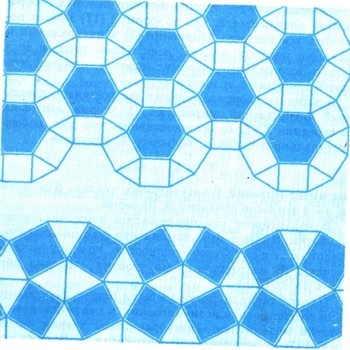
Если во всем искать математику, то можно построить интересную полезную математическую теорию, рассматривая, например, затейливые узоры на древнегреческой вазе или прихотливо повторяющиеся рисунки мозаик и паркета в старинных дворцах. Простейшая математическая теория ряда мозаик получится, если на плоскости рассматривать мозаики, состоящие из правильных многоугольников (см. рис.). Чтобы особо подчеркнуть важность того, что мозаики получаются повторением рисунка, введем следующее определение. Назовем преобразованием рисунка всякое его перемещение, которое надо совершить, чтобы совместить его с другим таким же рисунком. Оказывается, что для таких преобразований существует очень простая и красивая алгебра и такие преобразования образуют группу (более подробно о такой алгебре и теории групп см. в статье "Чем занимается алгебра?").

Эти преобразования можем подразделить на несколько видов: параллельный перенос рисунка, поворот его на какой-то угол и зеркальное отражение. При этом оказывается, что на плоскости для любых мозаик из правильных многоугольников может быть только 17 различных групп таких преобразований. Этот замечательный факт установил в 1891 г. знаменитый русский кристаллограф Е. С. Федоров.

Изучение мозаик дает богатую пищу не только для математических исследований, но и для воображения художника. На прилагаемом рисунке можно видеть как "портреты" некоторых абстрактных групп, так и мозаики другого типа. Эти остроумные рисунки сделал датский художник Мориц К. Ешер. Первое впечатление, что утки летят, а всадники скачут только слева направо. Но тут же глаз замечает, что такая же процессия с занимательной точностью движется в противоположном направлении. Художник предлагает каждому попробовать свои силы в составлении таких мозаик. Однако он предупреждает, что такая работа требует усидчивости! Интересно отметить, что для таких произвольных мозаик теория групп уже не является таким же удобным и плодотворным математическим аппаратом, как для правильных мозаик. Но здесь начинается применение другой любопытной математической теории, именно теории о покрытии плоскости без пропусков и наложений фигурами сложных очертаний. И эта математическая теория дает много интересных и полезных сведений всякому, кто познакомится с ней поближе.

Лист Мебиуса

Поверхность кольца, надеваемого на палец, имеет две стороны. Одной стороной она соприкасается с пальцем, вторая сторона наружная. У этих сторон две границы (два "рая), каждая имеет форму окружности. Если какая-нибудь букашка захочет переползти с наружной стороны кольца на внутреннюю, то она при этом непременно должна пересечь ту или другую границу. Немецкий математик А. Мебиус указал простую модель поверхности совсем другого фасона - односторонней поверхности. Ее легко приготовить, перекрутив на пол-оборота один конец прямоугольной бумажной полоски и приклеив его к другому концу той же полоски. Эту модель с той поры так и называют: лист Мебиуса.

Чтобы наглядно удостовериться в том, что у поверхности листа Мебиуса только одна сторона, возьмите карандаш и начните последовательно закрашивать лист, не отрывая карандаш от поверхности листа и не пересекая края листа. Когда вернетесь к тому месту, с которого начали, вы увидите, что окажется окрашенной вся поверхность листа, хотя его край вы и не пересекали ни разу.

Опыты с листом Мебиуса

Возьмите несколько листов плотной бумаги (например, обложки старых журналов большого формата), клей, ножницы и исследуйте "поведение" листа Мебиуса и других моделей, изготовляемых из прямоугольных полосок бумаги, если разрезать их по линиям вдоль края.

1. Что получится, если обыкновенное (неперекрученное) бумажное колечко разрезать вдоль его средней линии? Очевидно, два колечка, причем длина окружности каждого будет такой же, как длина окружности первоначально взятого колечка. А вот если лист Мебиуса мы также разрежем вдоль его средней линии, то образуется...

Проделайте и посмотрите, что получится.

2. Приготовьте второй лист Мебиуса из достаточно широкой полоски и разрезайте его ножницами так, чтобы линия разреза все время шла вдвое ближе к левому краю первоначальной полоски, чем " правому (линия разреза обойдет лист Мебиуса дважды). Теперь образуются два кольца, но они окажутся сцепленными. Проделайте!

А что получится, если вновь взять бумажную полоску, один ее конец перекрутить на полный оборот (на 360°), приклеить ж другому концу и разрезать получившуюся модель по средней линии?

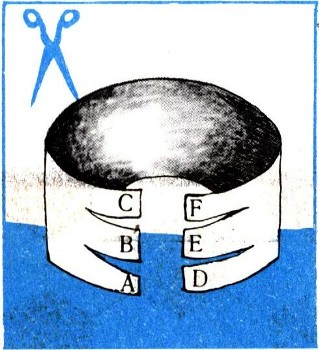
3. Надрежьте концы бумажной полоски поглубже. Склейте концы А и D. Пропустите конец В под А и приклейте его к Е. Пропустите конец С между В и А, а конец F между D и Е, после чего склейте концы С и F. Все склеивания концов производите прямо, т. е. без предварительного перекручивания.

Теперь каждый начатый разрез продолжайте вдоль всей модели; получится интересное переплетение трех колец: любые два будут сцеплены друг с другом и оба с третьим кольцом.

Если вы ошибетесь и конец С приклеете к концу F, не пропустив С между В к А, то после указанного разрезания получится обычная цепь из трех колец.

перейти к началу страницы