Решение задачи о раскрое фанеры

Теперь приступим к решению системы уравнений (3). Мы имеем три уравнения с пятью неизвестными. Поэтому два неизвестных будут свободными, а остальные три - зависимыми. Конечно, в качестве зависимых неизвестных нужно брать те неизвестные, у которых абсолютная величина коэффициентов минимальна.

Поэтому выберем в качестве свободных неизвестных x₁ и х₂ и выразим х₃, х₄, x₅ через х₁ и х₂. Для этого значение x₃ = 800 - х₁ - х₂ подставим в первые два уравнения, получим:

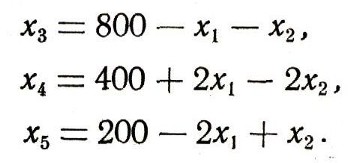
Теперь, давая х₁ и х₂ целые значения, получим всевозможные решения системы уравнений (3) в целых числах. Исследуйте самостоятельно, какие целые неотрицательные значения следует давать х₁ и x₂, чтобы x₃, x₄ и x₅ также были неотрицательными. Ниже приведена таблица некоторых решений системы (3).

Из таблицы видно, что листов фанеры достаточно и что самый выгодный способ раскроя будет при x₁ = 0, x₂ = 100, x₃ = 700. В этом случае образуются "лишние" заготовки еще для 100 изделий. В других случаях "лишние" заготовки будут некомплектными. Но нужно ли раскраивать все 800 листов? Ведь нужны заготовки для 1000 изделий, а не для 1100.

Поэтому практический интерес представляет следующий дополнительный вопрос к этой задаче: какое наименьшее число f листов фанеры следует взять со склада и какими из указанных способов следует кроить взятые листы, чтобы выполнить заказ? Для ответа на этот вопрос из всех решений в целых неотрицательных числах системы уравнений

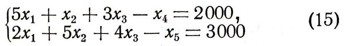
нужно выбрать такое решение (x₁, x₂, x₃, x₄, x₅), для которого f = x₁+x₂+x₃ принимает наименьшее значение, или, как мы будем говорить дальше, удовлетворяет условию минимальности.

Чтобы облегчить поиски, откажемся временно от требования, чтобы значения неизвестных были целыми. Попытаемся решить нашу задачу удачным выбором свободных неизвестных. Удобнее всего такими выбрать x₄, х₅ и какое-нибудь из неизвестных х₁, x₂, x₃. Определяя из уравнений (15) сначала, например, х₁, а затем x₂ и опуская промежуточные выкладки, будем иметь:

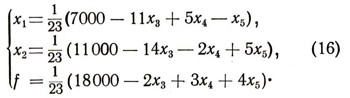
При данном значении х₃ наименьшее значение f мы получим, если неизвестным x₄ и x₅ дадим нулевое значение (это и понятно, ведь x₄ и x₅ - количество "лишних" заготовок!). Пусть х₄ = х₅ = 0. Легко видеть, что при возрастании значений неизвестного х₃ значение f будет убывать. Но рост x₃ сдерживается требованием, чтобы значения неизвестных х₁ и x₂ были неотрицательными. Так как

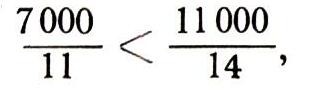
то из равенств (16) (при x₄=x₅ =0)

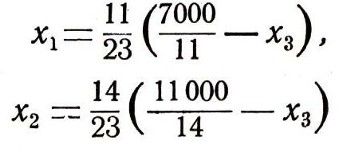
видно, что при возрастании х₃ отрицательные значения прежде всего будет принимать неизвестное х₁. Поэтому естественно неизвестное х₁ сделать свободным, а неизвестное x₃ - зависимым.

Определяя из уравнений (15) неизвестные х₂ и x₃, найдем:

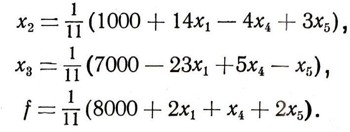
Легко видеть, что наименьшее значение f получим, если свободным неизвестным х₁, x₄ и х₅ дадим нулевые значения. При этом для зависимых неизвестных получим положительные значения:

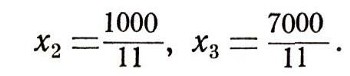
Следовательно, решение

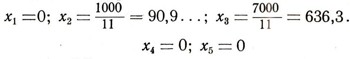
системы (15) удовлетворяет условию минимальности. Но нам требуется найти целочисленное решение в неотрицательных числах, удовлетворяющее условию минимальности. Из приведенных рассуждений следует, что для такого решения

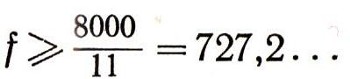
или даже f>=728, так как число f должно быть целым. Можно ожидать, что искомое решение мы полуним, если немного изменим значения неизвестных. Положим, например, x₁=0, x₂ = 91, x₃ = 637. Тогда

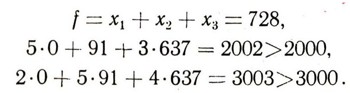
х₁	0	0	0	100	100	100	100	200	200	200	300	300
х₂	0	100	200	0	100	200	300	200	300	400	400	500
Х₃	800	700	600	700	600	500	400	400	300	200	100	0
Х₄	400	200	0	600	400	200	0	400	200	0	200	0
X₅	200	300	400	0	100	200	300	0	100	200	0	100

А это убеждает нас, что целочисленное решение с условием минимальности найдено. Итак, со склада достаточно взять лишь 728 листов фанеры и 91 из них кроить по второму, а остальные по третьему способу.

Решенная нами задача о раскрое фанеры относится к числу задач, составляющих предмет теории линейного программирования (см. стр. 413). В этой теории рассматривают задачи следующего типа: из всех решений в неотрицательных числах некоторой системы уравнений первой степени найти решение, удовлетворяющее условию минимальности. Иногда, как в задаче о раскрое фанеры, выдвигают дополнительное требование, чтобы значения неизвестных были целыми числами.

Весьма многие проблемы экономики, в частности вопросы планирования производства и перевозок, приводят к этим задачам.

перейти к началу страницы