Математика

Содержание раздела

Функции

Задание фигуры, состоящей из бесчисленного множества точек

Для задания фигуры Ф в этом случае стараются подыскать такое условие, которому: 1) удовлетворяют координаты х, у всех точек из Ф; 2) не удовлетворяет ни одна чужая точка (т. е. не принадлежащая Ф). То, что здесь сказано, станет понятнее на следующих примерах.

1. Подыщем условие для фигуры, состоящей из всех точек оси Ох. Координаты всех ее точек удовлетворяют уравнению у = 0, и, конечно, ни одна чужая точка ему не удовлетворяет, так как она лежит либо выше оси Ох (тогда y>0), либо ниже (тогда y<0). Уравнение y = 0 и служит искомым условием.

2. Все точки биссектрисы координатного угла хОу удовлетворяют уравнению х = у, и ни одна чужая точка. Биссектриса считается продолженной бесконечно в обе стороны.

3. Все точки внутренней части координатного угла хОу удовлетворяют системе неравенств х>0, y>0. Эта система служит условием, задающим фигуру Ф - внутренность угла хОу.

4. Все точки М (х; у) окружности радиуса 5 с центром в начале координат удовлетворяют уравнению х² + у² = 25, так как для любой ее точки расстояние от начала равно 5; ОМ = 5, или, на основании теоремы Пифагора, корень из x² + y²=5, что равносильно написанному выше уравнению. Для всех лежащих внутри окружности точек OM<5, т. е. x² + y²<25; для всех точек, лежащих вне окружности, OM>5, или x² + y²>25. Итак, для всех точек нашей окружности, и только для них, справедливо уравнение

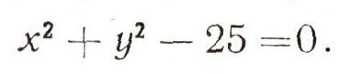
Уравнение, которому удовлетворяют все точки некоторой линии и не удовлетворяет ни одна посторонняя точка, называется уравнением этой линии; х, у в уравнении линии - текущие координаты.

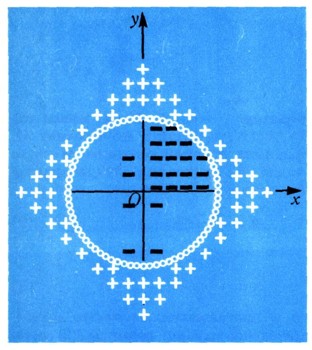
Отметьте на чертеже точки с целочисленными координатами, для которых левая часть х² + у² -- 25 > О, знаком " + "; те, для которых она отрицательна, з'наком " - "; точки, где она равна нулю, заключите в совсем маленький кружочек. Можно ограничиться, например, лишь теми целочисленными точками, для которых |х|+|y|=8. Проделав это, вы отчетливо поймете, что на координатной плоскости соответствует уравнению, что - неравенству (рис. 7).

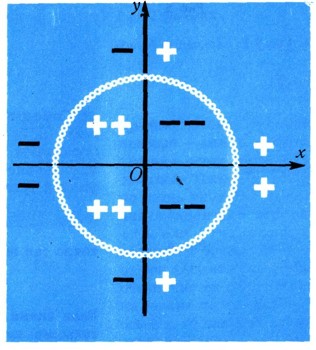
5. Уравнение х + у = 5 представляет собой уравнение прямой. Попробуйте доказать это сами! (Ниже будет показано, что всякое уравнение первой степени между х и у есть уравнение некоторой прямой.) Построить эту прямую (как и всякую) очень просто: достаточно подобрать две точки, удовлетворяющие этому уравнению, например (0; 5) и (1; 4), и затем, построив их, соединить линейкой. Снова заметим: прямая делит плоскость на две части, для одной из них (верхней) х + у>5, для другой х + у<5.

6. Попробуйте выяснить геометрический смысл неравенства |x|+|y|<5. Для этого сначала следует построить линию |x|+|y|=5. (Мы говорим: "Линия |x|+|y|=5"; это значит - линия, определенная уравнением |x|+|y|=5.) Она состоит из четырех частей. Построение следует вести отдельно в каждой из координатных четвертей: 1) при х>=0, у>=0; 2) при х<0, у >=0; 3) при х<0, у<0 и 4) при х>=0, y<0.

7. Уравнение х³ + ху² - 4х = 0 определяет фигуру, составленную из окружности и вертикальной прямой, проходящей через ее центр. Действительно, данное уравнение можно переписать так: x(x²+y²-4)=0, но произведение может быть равно нулю тогда, и только тогда, когда хоть один из множителей равен нулю, т. е. х = 0 или x² + y² - 4 = 0; первое есть уравнение оси Оу, второе - окружности (рис. 8).

8. Уравнение у = х² служит уравнением параболы. Построим ее по уравнению. Для этого напишем сначала таблицу, помещая в первой ее графе произвольные значения х: х= -3; -2,5; - 1; 0; 1; 2; 3; 4; ..., а во второй-соответствующие значения у: у = 9; 6,25; 1; 0; 1; 4; 9; 16; .... Если бы мы были в состоянии составить таблицу для всего бесконечного множества действительных чисел х и соответствующих у, а затем построили бы все такие точки (х; у), то эти точки сами заполнили бы собой всю искомую кривую (рис. 9). Фактически же мы вычислили координаты лишь точек: (-3; 9), (-2,5; 6,25), (-1; 1), (0; 0), (1; 1), (2; 4), (3; 9), (4; 16). Соединив их от руки плавной кривой (этим мы заполняем пробелы, соответствующие промежуточным значениям х, не включенным в таблицу), получим параболу, проходящую через эти точки. Конечно, это приблизительное построение; оно будет выполнено тем точнее, чем больше построим промежуточных точек.

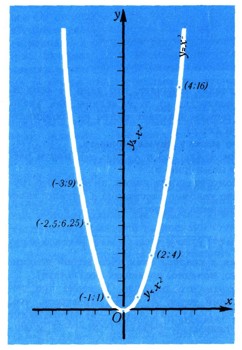
Заметим, что неравенство у>=х² определяет часть плоскости над параболой ("внутри" параболы), а неравенство у<x² - часть плоскости под ней ("вне" параболы).

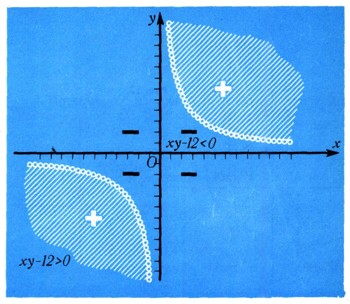
9. Уравнение ху = 12 (рис. 10) определяет на плоскости хорошо известную вам кривую - гиперболу (вспомните геометрическое изображение закона Бойля - Мариотта). Для ее построения решаем уравнение относительно y у=12/x и далее строим по точкам, как это делалось в предыдущей задаче.