Неопределенные системы уравнений первой степени

При решении в рациональных числах неопределенных систем уравнений первой степени с рациональными коэффициентами обычно пользуются методом последовательного исключения неизвестных. Решим, например, в рациональных числах такую систему уравнений:

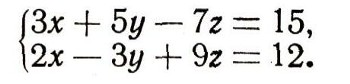
Из первого уравнения находим:

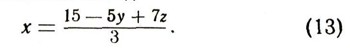
Подставляя значение неизвестного х во второе уравнение, получим:

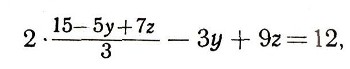
или

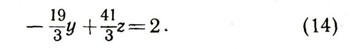
Давая в уравнении (14) неизвестному z какое-нибудь рациональное значение, т. е. принимая z за свободное неизвестное, а к и у за зависимые неизвестные, мы, пользуясь равенствами (14) и (13), сможем найти все решения в рациональных числах данной системы уравнений.

В целых числах такую систему можно решить сходным способом. Сначала рассматривают одно из уравнений системы и решают его в целых числах. Найденные выражения для неизвестных этого уравнения через некоторые вспомогательные целочисленные неизвестные подставляют во второе уравнение. Решив в целых числах полученное уравнение с новыми неизвестными, можно найти все решения в целых числах и данной системы уравнений.

перейти к началу страницы