Простейшие задачи

При решении геометрических задач координатным методом постоянно приходится опираться на несколько совсем простых стандартных задач: определение расстояния между точками, отыскание середины отрезка и др. При этом нужно иметь в виду, что выражение "дана точка" означает, что дано ее координатное обозначение (х; у), т. е. заданы два числа х, у. "Найти точку" означает найти ее координатное обозначение (х; у).

1) Расстояние между двумя точками.

Задача. Даны две точки А₁ (х₁; у₁) и А₂ (х₂; у₂)- Найти расстояние между ними (рис. 5).

Рис. 5.

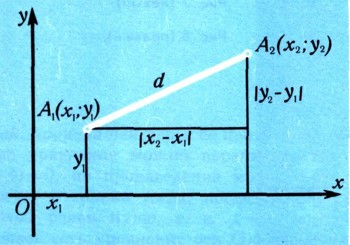
Проведя вспомогательные линии, читатель без труда убедится, что искомое расстояние d служит гипотенузой треугольника с катетами |х₂ - х₁|и |у₂ - у₁|, поэтому

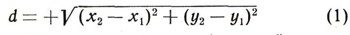
(при возведении в квадрат знак абсолютной величины опущен, что, конечно, не меняет результата). Важно заметить, что формула (1) верна при любом расположении точек А₁ и A₂. Проверьте, что, например, для A₁ ( - 1; - 2), A₂ (3; - 5) катеты будут действительно равны: |3-(-1)| и |(-5)-(-2)| и формула (1) дает:

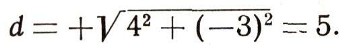
Для аналитической геометрии общность формул имеет очень большое значение. Благодаря этой общности при решении задач аналитически не нужно задумываться о том или ином расположении данных точек; можно решать задачу, даже не глядя на чертеж. Если чертеж и делается, то обычно лишь приблизительный, который служит только схемой, местом, куда записываются данные (координатные обозначения точек и пр.), а затем заносятся и найденные уже промежуточные и, наконец, окончательные результаты.

Рис. 6.

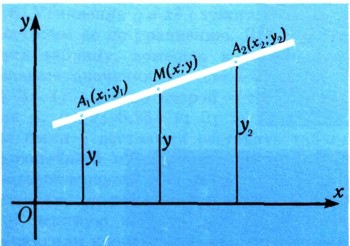
2) Середина отрезка. Даны концы отрезка A₁ (x₁; y₁), А₂ (х₂; у₂). Найти его середину М. Обозначим координаты искомой середины М через X, у. Из рис. 6 видно, что ордината у служит средней линией трапеции, поэтому

точно так же

Если знаки y_l и у₂ противоположны, то это доказательство неубедительно, однако формулы (2) остаются справедливыми во всех случаях. Проверьте это. Дан треугольник AВС: А (12; 6), В ( - 2; 4), С (6; -2). Найти длины его сторон и медиан. На оси Ох найти точку М, которая находилась бы от точки А (3; -1) на расстоянии, равном 5.

Решение. Обозначим координаты искомой точки М через (х; у). Она лежит на оси х, следовательно, у - О. Остается определить х. Записав аналитически (см. формулу (1)) условие задачи: AM = 5, получим уравнение для определения х.

Ответ: М (7,9...; 0) и М' (-1,9...; 0).

Задача 6. Найти точку М (х; у), находящуюся на равных расстояниях от осей координат и удаленную на 5 единиц от точки А (- 1; 6). Для определения х, у нужно лишь решить систему |х|= |у|, (х+ 1)² + (у - 6)² = 5². Всего четыре решения.

перейти к началу страницы