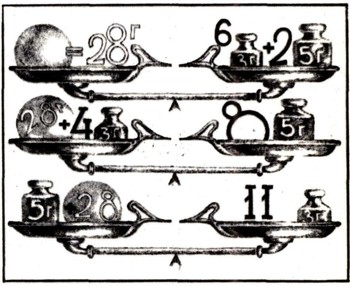
Решение задачи о взвешивании

Итак, нам нужно решить в целых числах уравнение (2). Определяем неизвестное х:

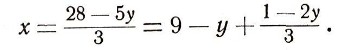
Верно и такое равенство:

Задача о взвешивании решена.

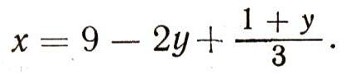
Им-то мы и воспользуемся. Ведь наша цель - уменьшить коэффициент при неизвестном. Введем обозначение :

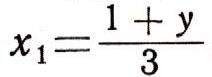
Задача сведена к решению в целых числах уравнения 3х₁- у = 1. Решая это уравнение, получим у=3х₁ - 1, где х₁- любое целое число. А тогда

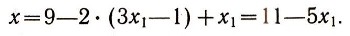
Таким образом, общее решение уравнения (2) можно записать так:

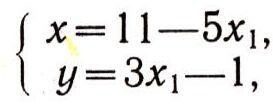
где x₁=0, ±1, ±2, ... .

Найдем несколько решений этого уравнения:

х₁	0	1	- 1	2	- 2	<3	>- 3
x	11	6	16	1	21	-4	26
y	- 1	2	-4	5	-7	8	- 10

Уравнение (2) имеет бесконечное множество решений, но мы сможем воспользоваться только некоторыми. Это зависит от числа гирь в нашем распоряжении да и размеров чаш.

Мы рассмотрели два уравнения первой степени. Каждое из них, как удалось установить, имеет целочисленные решения. Однако наряду с ними можно указать уравнения, которые решений в целых числах не имеют. Таково, например, уравнение Зx- 6y = 5. (11)

В самом деле, допустив, что при некоторых целых X и у равенство (11) верно, мы получим, что 5 делится на 3.

Какие неопределенные уравнения разрешимы в целых числах? Можно ли для всякого разрешимого в целых числах неопределенного уравнения первой степени найти его решение методом рассеивания?

На первый вопрос отвечает теорема: Уравнение с целыми коэффициентами а₁, а₂, ..., а_n, b

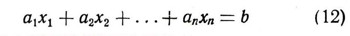
разрешимо в целых числах только в том случае, если свободный член Ь делится на наибольший общий делитель чисел а₁, а₂, ... а_n.

Ответим на другой вопрос: всегда ли предложенный метод решения в целых числах неопределенных уравнений первой степени приводит к цели?

Если а₁ - наименьший по абсолютной величине коэффициент при неизвестном в уравнении (12), то мы заменяем это уравнение другим, в котором все коэффициенты, кроме коэффициента а₁, заменены остатками от деления этих чисел на а₁. Если хотя бы один из коэффициентов а₂, a₃, ... а_n не делится на а\, то получим уравнение, коэффициенты которого по абсолютной величине меньше, чем у данного. С этим уравнением поступаем так же, как с данным. Если все числа а₂, а₃, ... а_п делятся на а₁, a b не делится, то данное уравнение неразрешимо. Если все числа a₂, a₃, ..., а_п и b делятся на а₁, то, деля обе части уравнения на а₁, получим уравнение, целые решения которого находятся без труда.

Из этого рассуждения следует, что описанный метод позволяет найти целые решения всякого разрешимого в целых числах неопределенного уравнения с целыми коэффициентами.

перейти к началу страницы