Рациональные и целые решения неопределенных уравнений первой степени. Метод рассеивания

Решить неопределенное уравнение первой степени с целыми или дробными коэффициентами в рациональных числах нетрудно. Возьмем, например, уравнение

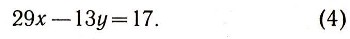
Чтобы найти все решения этого уравнения, узнаем, при каких рациональных значениях одного неизвестного соответствующее значение второго неизвестного рационально. Каждому значению неизвестного X соответствует единственное значение неизвестного у, определяемое из формулы:

Если значение неизвестного х рационально, то и значение неизвестного у, получаемое из формулы (5), рационально.

В формуле (5) роли неизвестных х и у различны. Неизвестному х мы даем произвольное значение, а значение неизвестного у находится в зависимости от выбранного значения неизвестного х. В соответствии с этим называют неизвестное х свободным, а неизвестное у зависимым. Уравнение (4) можно разрешить не только относительно неизвестного у, но и относительно неизвестного х. В таком случае неизвестное у станет свободным, а неизвестное х зависимым.

Для отыскания целых решений уравнения (4) мы не можем непосредственно воспользоваться формулой (5), так как при целых значениях одного неизвестного второе неизвестное не обязательно принимает целые значения. Чтобы найти все целые решения уравнения (4), найдем такие целые значения неизвестного х, для которых соответствующее значение неизвестного у является целым числом.

Задача о раскрое фанеры - одна из задач бурно развивающейся в настоящее время теории линейного программирования

Это незначительное на первый взгляд изменение постановки задачи открывает путь для ее решения. Замечая, что

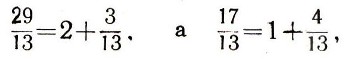
и пользуясь формулой (5), получим:

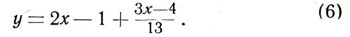
Мы должны узнать, при каких целых значениях неизвестного х неизвестное у принимает целые значения. Так как при целом х число 2х - 1 является целым, то из формулы (6) следует, что неизвестное у при целом х только в том случае принимает целое значение, если выражение

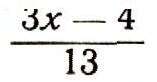
есть целое число. Задача еще не решена, но мы близки к цели. В самом деле, полагая

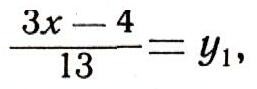
замечаем, что вопрос, при каких целых значениях неизвестного X неизвестное у принимает целые значения, равносилен вопросу о целых решениях уравнения

Таким образом, решение в целых числах уравнения (4) удалось свести к решению в целых числах уравнения (7). Чем же второе уравнение предпочтительнее первого?

Самым простым из неопределенных уравнений первой степени естественно считать такое, у которого хотя бы один из коэффициентов при неизвестных равен 1 или -1. В этом случае неизвестное с таким коэффициентом при любых целых значениях остальных неизвестных принимает целые значения. Поэтому чем меньше наименьшая из абсолютных величин коэффициентов при неизвестных, тем уравнение предпочтительнее. В уравнении (4) наименьшая из абсолютных величин коэффициентов при неизвестных равна 13, а в уравнении (7) равна 3. Как удалось достичь этого? Коэффициент при неизвестном х и свободный член уравнения были заменены остатками от деления этих чисел на 13. Но остаток от деления целого числа на натуральное число всегда меньше этого натурального числа. Понятно, почему с самого начала неизвестное у было выражено через неизвестное х: мы выбрали неизвестное с наименьшим по абсолютной величине коэффициентом. Теперь ясно, как поступать с уравнением (7).

"Метод рассеивания" глазами художника.

При каких целых значениях неизвестного у₁ неизвестное х принимает целые значения? Из условия

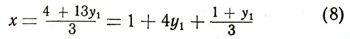
находим, что неизвестное х при целых значениях неизвестного y_lтолько в том случае принимает целые значения, если

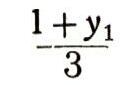
есть целое число. Обозначая через x₁ это выражение, получим 1+y_l=3x₁, или

Таким образом, задача сведена к решению в целых числах уравнения (9). Решить в целых числах уравнение (9) - значит узнать, при каких целых значениях неизвестного х\ неизвестное y_l принимает целые значения. Но y₁ = 3x₁ - 1, поэтому y_lпринимает целые значения при любых целых значениях неизвестного х₁Из равенств (8) и (6) последовательно найдем выражения для неизвестных х и у.

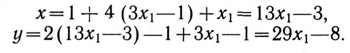
Из приведенных рассуждений следует, что формулы

при x₁ = 0, ±1, ±2, ±3, ... дают все целые решения уравнения (4).

Аналогично решается уравнение с тремя и более неизвестными. Показанный на примере метод решения неопределенных уравнений в целых числах несущественно отличается от метода, предложенного индийцами. В связи с тем что при решении неопределенного уравнения по этому методу оно сводится к цепи уравнений с уменьшающимися коэффициентами, индийские математики назвали этот метод методом рассеивания.

перейти к началу страницы