Что такое координаты и для чего они служат

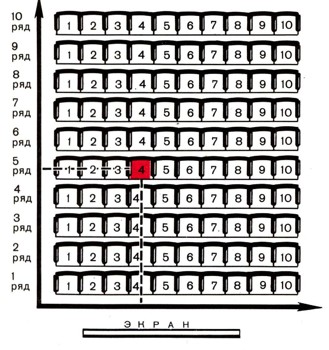
Когда приходится иметь дело с большим числом (а тем более с бесконечным множеством) предметов, для различения их друг от друга удобно называть их не случайными именами (Ваня, Маша, Лондон, Амазонка,..), а так, чтобы по каждому "имени" легко было отыскать соответствующий ему предмет и, наоборот, для каждого предмета легко узнать его "имя" в данной системе наименований. Адрес: "Такой-то переулок, дом 7, квартира 6" - много удобнее, чем то, как писали еще в начале нашего века: "Дом Жукова, квартира Еремеева". На билете написано: "Ряд 5, место 4", или, короче, "5, 4"; эта надпись заменяет "имя" кресла зрительного зала (рис. 1), а сами числа 5, 4 называются его координатами (заметьте, что "4, 5" - это совсем другое кресло: важен порядок). Почти так же просто дать "имя" каждой точке, например, того листа книги, который вы сейчас читаете: расстояние этой точки от левого края листа обозначим через х, расстояние от нижнего края - через у и будем считать пару чисел (х, у) названием этой точки. Измеряя расстояния в сантиметрах, верхнему правому углу страницы дадим "имя" (20, 26), нижнему правому - (20, 0), центру листа -(10, 13). Все точки листа (а их бесконечно много!) получат свои "имена". Подобным же образом каждая точка вашей комнаты получит свое "имя" (х, у, z), здесь х - расстояние (в метрах) от северной стены, у - расстояние от западной стены, z - расстояние точки от пола; вы легко найдете, например, точку (3, 2, 1). Координата х для точки, находящейся за северной стеной, считается отрицательной, так же как у - для точки за западной стеной и z - для точки нижних этажей. Те плоскости, от которых отсчитываются расстояния х, у, z, называются координатными плоскостями (на каждой из них одна координата равна нулю), а линии их пересечения - осями координат; например, прямая, вдоль которой у к z равны нулю, называется осью х.

Рис. 1

Читатель, вероятно, хорошо знает, что такое долгота и широта места на поверхности Земли. Это географические координаты. Так, долгота Москвы + 37,5° (значит, к востоку от Гринвичского начального меридиана), а широта +55,8° (значит, к северу от экватора), поэтому координатное обозначение Москвы записывается так: 37,5°, 55,8°. Координаты в геометрии. Числа играют важную роль в геометрии. При их помощи мы оцениваем размеры предметов. Длины, площади, объемы после выбора единицы измерения выражаются числами. Можно ли при помощи чисел описать форму предметов, форму самых причудливых фигур? Мы знаем, что углы треугольника определяют его форму ("два треугольника с равными углами подобны", т. е. имеют одинаковую форму), значит, в некоторых случаях числа могут охарактеризовать форму, в данном случае два числа - два угла. Но можно ли форму любой фигуры описать при помощи чисел? Положительный ответ дает координатный метод, введенный в математику в середине XVII в. французскими учеными П. Ферма и Р. Декартом.

Идея метода координат используется в шахматах (в шахматной нотации).

Идея координат существовала задолго до Ферма и Декарта, ее можно проследить еще в древнем мире: в незапамятные времена художники пользовались координатной сеткой для перенесения изображений на другую плоскость; вероятно, еще древнее вышивание по канве, которая представляет собой, так сказать, материализованную координатную сетку. Сферическими координатами (долготой и широтой) пользовались астрономы древнего Вавилона и Египта.

Координатный метод - это способ изучения фигур аналитически, т. е. при помощи вычислений. Ветвь геометрии, изучающая фигуры этим способом, называется аналитической геометрией. Чтобы изучать фигуры, нужно прежде всего уметь точно описывать их. Описание должно быть полным: прочтя такое описание, мы должны суметь по нему восстановить фигуру, т. е. построить фигуру точно такую, как та, с которой было составлено описание. Говорят, что таким описанием фигура задана (однозначно), а само описание называют заданием фигуры. Геометрическую фигуру будем представлять себе состоящей из точек: фигура - это множество точек (конечное или бесконечное). Если фигура Ф состоит из конечного числа точек (или конечным числом точек однозначно определяется, например многоугольник - своими вершинами), то для ее полного описания достаточно задать каждую точку. И в случае бесконечного множества точек нужно уметь задавать положение отдельных точек. Для простоты рассмотрим точки и фигуры на плоскости.

перейти к началу страницы