Раскрой фанеры

В деревообделочный цех одного завода поступил заказ вырезать из фанеры заготовки двух видов для 1000 изделий. Известно, что на одно изделие идет две заготовки первого вида и три второго. На складе имеется 800 листов фанеры одного образца. Были предложены три способа раскроя этих листов. При первом способе из листа фанеры получается пять заготовок первого вида и две второго, при втором -одна заготовка первого вида и пять второго и, наконец, при третьем - три заготовки первого вида и четыре второго.

Достаточно ли для выполнения заказа листов фанеры, имеющихся на складе? Сколько листов фанеры нужно кроить по первому, сколько по второму и по третьему способам, чтобы выполнить этот заказ?

Обозначим буквами х₁, х₂, x₃ соответственно число листов фанеры, раскроенных по первому, второму и третьему способам. Тогда 5х₁ +х₂ + x₃ - количество полученных заготовок первого вида и 2х₁ + 5x₂ 4х₃- количество полученных заготовок второго вида. Так как для выполнения заказа требуется не менее чем 2000 заготовок первого и 3000 заготовок второго вида, то должны выполняться неравенства:

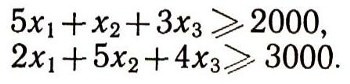
Чтобы заменить неравенства строгими равенствами, обозначим через x₄ количество заготовок первого вида, которых придется изготовить сверх 2000, а через х₅ - количество "лишних" заготовок второго вида. Тогда, учитывая, что x₁+x₂ + x₃ = 800, получим следующую систему уравнений:

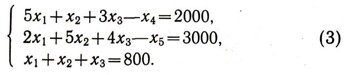
Конечно, x₄ и х₅ так же как и х₁, x₂, x₃, должны быть целыми неотрицательными числами. Каждому варианту (х₁, х₂, x₃) распределения 800 листов фанеры по способам раскроя соответствует решение (х₁, x₂, х₃ х₄, x₅) системы уравнений (3) в целых неотрицательных числах. Наоборот, каждому решению (x₁, x₂, x₃, х₄, х₅) системы (3) в целых неотрицательных числах соответствует определенный вариант распределения 800 листов фанеры по способам раскроя. Поэтому задача о раскрое фанеры приводит к отысканию решений системы (3) в целых неотрицательных числах.

перейти к началу страницы