Равна ли сумма углов треугольника 180°

Оставим пока в стороне вопрос о том, включать ли аксиому (А) в число аксиом геометрии, предназначенной для описания мира световых лучей. Укажем лишь, что именно с помощью аксиомы (А) в школьном учебнике доказывается теорема: (В) Сумма внутренних углов любого треугольника равна 180° (в радианной мере л).

Несколько сложнее доказывается обратная теорема: Если сумма внутренних углов хотя бы одного треугольника в точности равна 180°, то справедлива аксиома о параллельных, т. е. через точку А невозможно провести в плоскости две различные прямые, не пересекающие данную прямую а, которая лежит в той же плоскости.

Таким образом, из аксиомы о параллельных следует, что сумма внутренних углов любого треугольника равна 180°; наоборот, из того, что сумма углов некоторого треугольника равна 180°, следует аксиома (А). Значит, в списке аксиом евклидовой геометрии можно вычеркнуть аксиому о параллельных, но вместо нее внести предложение (В). При этом все остальные теоремы евклидовой геометрии остались бы неизменными.

Мы выше пояснили трудность (даже практическую невозможность) проверки аксиомы о параллельных в мире световых лучей. Если бы даже можно было выделить сколь угодно тонкий пучок световых лучей и если бы не было никакого их поглощения, то и тогда совершенно непонятным оставалось бы их поведение за пределами видимости современных телескопов. Всегда неясным оставался бы вопрос о том, пересекутся ли лучи а и b', если угол Ф близок к 90° (рис. 6). Сказать, что лучи будут и дальше идти по прямой, - значит, вообще ничего не сказать, ибо свойства прямой, которые кладутся в основу рассматриваемой сейчас нами геометрии, выводятся на основании изучения свойств реального мира световых лучей, а не наоборот.

Приняв аксиому (А), мы получим геометрию, в которой сумма углов любого треугольника равна 180°. Приняв предложение, противоположное аксиоме (А), мы получим геометрию, в которой сумма углов всякого треугольника отлична от 180°. Как же здесь быть? Принимать или не принимать аксиому (А)?

Ввиду чрезвычайных трудностей, связанных с экспериментальной проверкой аксиомы (А) в опытах со световыми лучами, возникает вопрос о том, не проще ли на таких опытах проверять предложение (В). Поясним подробнее возникающее здесь положение.

Представим себе, что на местности (см. рис. 4) ведутся геодезические работы. Пусть в пункте В на штативе укреплен шарик, который геодезист наблюдает в обычный теодолит, установленный в пункте А.

Какой же величины надо взять шарик в пункте В для этих наблюдений? Шарик надо выбрать так, чтобы его изображение получилось с возможной точностью в центре окуляра теодолита. Если шарик таков, что его изображение будет большим кружком, его надо уменьшить для более точной наводки. Значит, шарик не должен быть слишком большим. Уменьшать шарик, однако, имеет смысл лишь до тех пор, пока это уменьшение сказывается на точности наводки теодолита. Если чувствительность прибора не даст возможности улучшить наводку путем дальнейшего уменьшения шарика, такое уменьшение просто бесполезно. Выбрав шарик надлежащего размера, геодезист считает, что он имеет дело с "точками" А ч В, соединенными отрезком АВ. При этом, как и выше, шарик В может на самом деле быть довольно большим (это зависит, разумеется, от расстояния АВ).

Теперь представим себе, что в пункте С также установлен на штативе шарик надлежащих размеров. Поочередно наводя теодолит на шарики В и С, геодезист находит величину а, равную разности отсчетов на лимбе теодолита.

Как указывалось выше, геометрия оперирует абстрактными понятиями точки, прямой, треугольника и т. д. Поэтому наш геодезист, выполнив конкретный физический эксперимент с шариками и снопиками световых лучей, рассматривает абстрактный треугольник ABC и считает, что величина угла в вершине А равна а - разности отсчетов на лимбе теодолита.

Понятно, что величина а. зависит от того, насколько хорошим и совершенным был примененный теодолит. Поэтому, применяя различные измерительные приборы, геодезист должен был бы каждый раз изучать другой абстрактный треугольник ABC. Представим себе для определенности, что конструкция теодолита не дает возможности фиксировать показания на лимбе более мелкие, нежели 10'. В таком случае, выполнив отсчет на лимбе после наведения на шарик В, говорят, что отсчет сделан с точностью до 10'. То же самое относится и к наводке теодолита на шарик С.

Найдя разность отсчетов а, геодезист считает, что, применив другой, более точный теодолит, он мог бы получить другую разность, однако ее отличие от а не превысит 20'. Таким образом, рассматривая абстрактный треугольник ABC с углом А, равным а, геодезист вправе считать, что, применяя более точные приборы, он мог бы получить для угла а; другую величину, лежащую в пределах от а -20' до а +20'.

Аналогично можно для углов В та С получить величины b и y и найти сумму

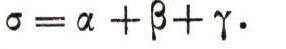
Возникает вопрос: равна ли эта сумма 180°? Понятно, что такое совпадение маловероятно. Вспомним прежде всего, что каждая наводка теодолита выполнялась с точностью до 10'. Для определения з теодолит пришлось наводить 6 раз. Поэтому применение более точного прибора могло бы привести к получению другой суммы, находящейся в промежутке от б -1° до б +1°.

Итак, определение суммы углов рассматриваемого абстрактного треугольника зависит от точности проведенных измерений (в данном случае от точности теодолита). В нашем случае геодезист вправе рассмотреть абстрактный треугольник, сумма углов которого отличается от найденной при измерении величины з, но не более чем на 1°.

Здесь возникает другой вопрос: насколько измеренная сумма углов б отличается от 180°? Превосходит ли это отличие 1°? Находится ли разность между 180° б пределах точности примененных инструментов? Иными словами, может ли геодезист в данном случае рассматривать абстрактный треугольник с суммой углов 180°?

Проанализируем возможные результаты измерения. Здесь имеются две возможности.

1. В результате измерения получилась сумма б = а + b + y, отличие которой от 180° превосходит точность проведенных измерений (в данном случае 1°). В этом случае геодезист должен рассуждать примерно так. Если принять аксиому (А), в нашей геометрии сумма углов всякого треугольника будет равна 180°. Проведенный же опыт показывает, что принятая точность измерений не согласуется с таким выводом. Это означает, что такая геометрия для нашего геодезиста недостаточно хороша. Выводы ее он не смог бы применять в своей практике.

Зная длину АС, углы а и y, он не смог бы с необходимой точностью, как это описано выше, определить длину АВ, ибо теорема Пифагора и признаки подобия треугольников справедливы лишь там, где сумма углов треугольника равна 180°. Ему пришлось бы для практических потребностей строить геометрию, где аксиома (А) не справедлива и, следовательно, сумма углов треугольника не равна 180°.

2. Сумма углов б = а+ b + y, полученная в результате измерения, отличается от 180° на величину, не превосходящую точность измерений (в данном случае 1°). В этом случае геодезисту для практических нужд вполне пригодна геометрия, в которой сумма углов треугольника равна 180°. У него нет никаких оснований отвергать аксиому (А), а равно и предложение (В). Обычная евклидова "школьная" геометрия здесь оказывается весьма полезной, ее выводы приобретают большое практическое значение с точностью, принятой в измерениях нашего геодезиста.

Однако необходимо заметить, что геодезист и в данном случае не должен слишком пренебрежительно относиться к геометрии, где неверна аксиома (А) и где сумма углов треугольника отлична от 180°. Не исключена возможность, что и такая геометрия в будущем окажется ему полезной. Если все измерения геодезиста пока хорошо согласовывались с той геометрией, где сумма углов треугольника равна 180°, то, может быть, в дальнейшем, увеличив точность приборов или измеряя углы значительно больших (космических) треугольников, он столкнется с тем, что при новых измерениях обычная геометрия уже не будет описывать мир с достаточной точностью. И тогда понадобится совсем другая геометрия.

Итак, вопрос заключается лишь в том, какая геометрия с большей точностью описывает мир световых лучей, какой мысленный слепок с реального мира является более точным.

Вполне владея изложенными идеями, Н. И. Лобачевский уже в первой половине XIX в. имевшимися в то время астрономическими средствами измерил сумму углов весьма большого космического треугольника. За вершины были взяты две самые удаленные точки на эллиптической орбите Земли и одна из далеких звезд. В результате измерения получилась величина, как и следовало ожидать, отличная от 180°, однако это отличие не выходило за пределы точности примененных инструментов. Таким образом, вопрос о том, какая геометрия точнее описывает мир световых лучей, остался открытым. Было неясно, понадобится ли вообще когда-нибудь геометрия, в которой не имеет места аксиома (А). Не является ли такая геометрия бесполезным плодом фантазии?

перейти к началу страницы