Пифагоровы треугольники

Футбольное поле - это прямоугольная площадка длиной примерно 90 м и шириной 60 м. Как разметить такую площадку? Прямоугольник на листе бумаги строят при помощи линейки и циркуля или линейки и угольника. Эти приборы слишком малы для работы на местности. Они не обеспечат нужной точности в построении прямых углов такой площадки, как футбольное поле. Если же сделать циркуль и угольник достаточно больших размеров, то ими будет невозможно пользоваться.

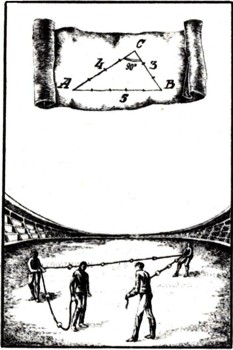
С давних времен известен очень простой способ построения на местности прямых углов. Выполним такое построение. Возьмем шнур и три колышка. На шнуре отметим 12 равных долей. Затем узлами выделим три части шнура MB, ВС, CN так, чтобы первая часть состояла из пяти, вторая из четырех и последняя из трех таких долей. Узлы М и N свяжем вместе и обозначим вновь полученный узел через А.

С помощью колышков натянем часть шнура ВС вдоль данной прямой так, чтобы точка С совпала с точкой, через которую должен быть проведен перпендикуляр к данной прямой. Потом оттянем шнур за узел А так, чтобы участки АВ и АС стали прямолинейными, и вобьем в точке, где будет находиться узел А, колышек. Задача построения на местности прямого угла нами решена, так как угол АСВ прямой.

Чтобы убедиться в этом, докажем, что прямоугольным будет всякий треугольник, стороны которого, измеренные какой-нибудь единицей измерения, выражаются числами 3, 4 и 5. Для доказательства возьмем прямоугольный треугольник с катетами, равными двум меньшим сторонам данного треугольника, и найдем его гипотенузу х. По теореме Пифагора x² = 3² + 4². Поэтому х = 5. Таким образом, три стороны данного треугольника соответственно равны трем сторонам прямоугольного треугольника. А отсюда следует, что и данный треугольник прямоугольный.

Доказанное свойство треугольника со сторонами 3, 4 и 5 было, по-видимому, известно еще древнеегипетским землемерам: такой треугольник называют египетским. Всякий целочисленный треугольник (т. е. такой, длины сторон которого выражаются целыми числами), подобный египетскому, также является прямоугольным.

Существуют ли другие целочисленные прямоугольные треугольники?

Циркулем и угольником таких размеров невозможно было бы пользоваться

Построение прямого угла на местности

Если катеты и гипотенузу какого-нибудь целочисленного прямоугольного треугольника обозначить буквами х, у и г, то по теореме Пифагора получим:

Можно доказать, что верно и обратное, т. е. если х, у и z - натуральные числа, удовлетворяющие уравнению (1), то треугольник со сторонами х, у и z прямоугольный. Целочисленный прямоугольный треугольник для краткости иногда называют пифагоровым.

Наше рассуждение показывает, что задача отыскания всех пифагоровых треугольников сводится к решению уравнения (1) в натуральных числах. Рассмотрим несколько других задач.

перейти к началу страницы