Аксиома о параллельных

Выбрав систему аксиом, начинают доказывать теоремы все более и более сложные. Весьма просто, например, с помощью теоремы о внешнем угле треугольника доказывается такая теорема планиметрии: Две прямые, перпендикулярные третьей прямой, не пересекаются.

Дадим следующее определение: Две прямые, лежащие в одной плоскости и не пересекающиеся, называются параллельными.

Пусть на плоскости даны прямая а и точка А (рис. 6). Ясно, что через точку А можно провести прямую b, параллельную а. Для этого достаточно опустить из точки А перпендикуляр А В на прямую а, а затем из точки А провести прямую b, перпендикулярную АВ. Это и будет искомая параллельная. Итак, параллельные прямые существуют!

Рис. 6

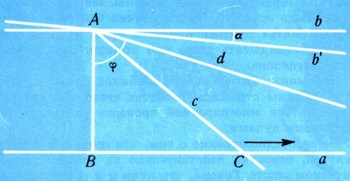
Теперь возникает вопрос: нельзя ли через точку А провести еще одну прямую b', также параллельную прямой а? (Напомним, что все происходит на одной плоскости, т. е. мы занимаемся только планиметрией.) Тому, кто не думал над этим раньше, не изучал этого вопроса, хочется немедленно и категорически ответить: "Нет, нельзя! Прямая b' пересечет прямую а, возможно, очень далеко, но непременно пересечет!" Воздержимся пока от столь категорического ответа и постараемся вдуматься в поставленный вопрос глубже.

Возьмем на прямой а точку С и соединим ее с точкой А прямой с. Затем будем передвигать точку С вправо по прямой а. При этом прямая с будет поворачиваться около точки А. Ясно, что прямая с никогда не сольется с прямой b, ибо b с а не пересекается. Но прямая с, поворачиваясь в одном и том же направлении, будет неограниченно приближаться к какому-то определенному предельному положению, когда точка С неограниченно удаляется вправо. Теперь спросим себя: будет ли прямая b той предельной прямой, к которой неограниченно приближается прямая с? Или, может быть, прямая с будет неогра-. ничейно приближаться к предельной прямой b', отличной от b, так что прямая с, поворачиваясь, не сможет войти внутрь угла а? Опять хочется отвергнуть это предположение.

Однако подумаем еще. Проведем из точки А луч d под углом ф<90° к прямой АВ. Если этот угол мал, прямые а и d пересекутся на чертеже. Если же увеличить угол ф (см. рис. 6), прямые а и d пересекутся уже не на чертеже, а где-то за полем книги. Еще немного увеличим угол ф. Тогда прямые a и d будут пересекаться дальше, скажем на расстоянии нескольких сотен метров. Ясно, что практически убедиться в этом весьма трудно, почти невозможно, но принципиально мыслимо.

Еще увеличим угол ср. Пусть он отличается от 90°, допустим, на одну миллионную долю градуса. Что в этом случае можно сказать о пересечении прямых а и d? Хочется их изображения мысленно продолжить. Но так ли хорошо мыслим мы это продолжение? Не теряет ли смысл этот мысленный эксперимент? Ведь если угол ср достаточно близок к 90°, то "продолжать" прямые придется туда, куда не удавалось заглядывать даже при помощи самых мощных телескопов.

Напомним, что аксиомы изучаемой сейчас геометрии должны отражать свойства световых лучей и подвергаться многократной проверке на опытах со световыми лучами. Наше предположение о том, что лучи a и d пересекутся, основано действительно на большом практическом опыте. Говоря, что лучи а и d пересекутся даже очень далеко (например, на расстоянии 100 млн. км), мы базируемся на большом опыте астрономических наблюдений.

Предположение же о том, что лучи света а и d пересекутся за пределами видимости самых мощных телескопов, уже основано на чистой фантазии. Ведь неизвестно, как там поведут себя лучи света. Здесь уже нет никаких оснований ссылаться на эксперимент. Мы договорились, что эталон прямизны - это луч света. Чтобы сделать какое-либо заключение о поведении прямых а и d, надо знать физические свойства световых лучей.

Одним из видов "движения" является симметрия (см. рис. на стр. 299). Фигуры, которые в результате движения переходят в себя, называются симметричными. На рисунке изображены фигуры, обладающие осевой, центральной симметрией и симметрией порядка "n" (говорят, что фигура обладает симметрией порядка "n",т если она переходит в себя при повороте вокруг точки - центра симметрии - на угол 360/n градусов).

Определите, к какому из этих трех видов симметрии относится каждая фигура, найдите ось или центр симметрии, а для фигур с симметрией порядка "n" найдите это число. Приготовьте 3 ящика, 3 белых и 3 черных шарика. Положите в первый ящик 2 белых шарика и наклейте этикетку "Б-Б"; во второй ящик положите 2 черных шарика и наклейте этикетку "Ч-Ч"; в третий ящик положите белый и черный шарики и наклейте этикетку "Б-Ч".

Уйдите из комнаты, а ребятам предложите заново разместить шарики по два в каждый ящик так, чтобы все этикетки неправильно указывали содержимое ящиков. Пусть ребята прикроют ящики, чтобы вам, когда вернетесь в комнату, были видны только этикетки, но не шарики. Теперь, вытащив только один шарик из какого-то одного ящика, вы беретесь точно определить, какие шарики находятся в каждом ящике.

Но если хотите удачи, то, разумеется, вам надо сначала обдумать, из какого ящика вы должны вытаскивать шарик и как надо рассуждать, чтобы, зная цвет вытащенного шарика, точно установить, какие шарики находятся в каждом ящике. Итак, вопрос о том, можно ли через точку А провести две прямые b и b', параллельные а, зависит от свойств световых лучей. Ясно, что, если угол ф очень близок к 90°, экспериментальная проверка того, пересекутся ли лучи а и d, невозможна.

Следует хорошо уяснить, что вопрос о том, можно ли из точки А провести только одну прямую, не пересекающую прямую а, решается не так уж просто. Ничего категорически здесь сразу сказать нельзя.

Разумеется, неочевидность какого-либо утверждения ни в коей мере не означает его несправедливости. Ведь теорема Пифагора, например, тоже не так уж очевидна: совсем не сразу можно поверить в то, что площадь квадрата, построенного на гипотенузе любого прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах. Чтобы убедиться в справедливости теоремы Пифагора для любого прямоугольного треугольника, ее доказывают. Доказательство это опять-таки основывается на тех же аксиомах.

Возможно, в нашем вопросе положение аналогично. Иными словами, можно ли доказать исходя из принятых аксиом такое предложение: (А) Через точку вне прямой нельзя провести более одной прямой, параллельной данной.

Возможно, что еще Евклид задавался этим вопросом, однако ответа на него у Евклида нет. Но так как этим предложением (или эквивалентным ему) приходилось пользоваться при доказательстве других теорем, пришлось принять предложение (А) за аксиому. (Евклид в качестве аксиомы принял другое предложение, которое, однако, равносильно предложению (А).) В стабильном учебнике предложение (А) названо аксиомой о параллельных. Итак, принимают новую аксиому, хотя, как объяснялось выше, есть все основания усомниться в ее справедливости в мире световых лучей.

перейти к началу страницы