Математика

Содержание раздела

ЧИСЛА И ФИГУРЫ

Позиционные системы

Первой известной нам позиционной системой счисления была шестидесятеричная система вавилонян, возникшая примерно за 2500-2000 лет до н. э. Основанием ее служило число 60. Следовательно, в ней должно было бы быть 60 цифр. А таблица умножения должна была состоять из 60*60/2=1800 строк.

Как же вавилоняне записывали свои цифры и как запоминали такую чудовищную таблицу умножения? Вавилоняне поступали так: записывали все числа от 1 до 59 по десятичной системе, применяя принцип сложения. При этом они пользовались всегда двумя знаками:

прямым клином для обозначения 1 -

и лежачим клином для 10 -

Число 32, например, писали так:

Эти знаки и служили цифрами в их системе. Число 60 снова обозначалось тем же знаком, что и 1, т. е.

Так же обозначались и числа 3600, 60³ и все другие степени 60. Например, число 92 записывали так:

Таким образом, "цифры", т. е. все числа от 1 до 59, вавилоняне записывали по десятичной непозиционной системе, а число в целом - по позиционной системе с основанием 60. Поэтому-то мы называем их систему шестидесятеричной (а не шестидесятичной, как нужно называть, учитывая только одно основание 60).

Но нумерация вавилонян имела и еще одну важную особенность: в ней не было знака для нуля. И если был изображен прямой клин

то без дополнительных пояснений нельзя было определить, какое число записано: 1, 60, 3600 или какая-нибудь другая степень 60. Запись числа 92, приведенная выше, могла обозначать не только 92=60 + 32, но и 3600+32=3632. Она могла также означать

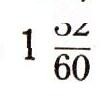
или

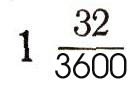
и т. д.

Таким образом, запись в вавилонской нумерации не носила абсолютного характера - для определения абсолютного значения числа нужны были еще дополнительные сведения. Впоследствии вавилоняне ввели специальный символ для обозначения пропущенного шестидесятичного разряда. Например, число 3632 нужно было бы записать так:

Но в конце числа этот символ обычно не ставился.

Таблицу умножения вавилоняне никогда не запоминали - это было почти невозможно. Они пользовались при своих вычислениях готовыми таблицами умножения, так же как мы теперь пользуемся, например, таблицами логарифмов.

Шестидесятеричная система вавилонян сыграла большую роль в развитии математики и астрономии. Следы ее сохранились до наших дней. Так, мы до сих пор делим час на 60 минут, а минуту на 60 секунд. Точно так же, следуя примеру вавилонян, окружность мы делим на 360 равных частей (градусов).

В начале нашей эры индейцы племени майя, которые жили на полуострове Юкатан в Центральной Америке, пользовались другой позиционной системой - с основанием 20. Свои цифры индейцы майя, как и вавилоняне, записывали, пользуясь принципом сложения. Единицу они обозначали точкой, а пять -горизонтальной чертой (см. рис.), но в этой системе уже был знак для нуля. Он напоминал по своей форме полузакрытый глаз. Например, число 20 индейцы майя записывали при помощи знака для единицы и внизу знака для нуля (числа писали не в строчку, а столбцами).

Десятичная позиционная система впервые сложилась в Индии не позднее VI в. н. э. Здесь же был введен наш символ для нуля. Итак, позиционные системы счисления возникли независимо одна от другой в древнем Двуречье, у племени майя и, наконец, в Индии. Все это говорит о том, что возникновение позиционного принципа не было случайностью.

Каковы же были предпосылки для его создания? Что привело людей к этому замечательному открытию? Чтобы ответить на эти вопросы, мы снова обратимся к истории. В древнем Китае, Индии и в некоторых других странах существовали системы записи, построенные на мультипликативном принципе.

Пусть, например, десятки обозначаются символом X, а сотни - С. Тогда запись числа 323 схематично будет выглядеть так: ЗС2ХЗ.

В таких системах для записи одинакового числа единиц, десятков, сотен или тысяч применяются одни и те же символы, но после каждого символа пишется название соответствующего разряда. На аналогичном принципе основаны наши счеты: одно и то же количество косточек означает число десятков, сотен, тысяч и т. д., в зависимости от того, в каком ряду расположены эти косточки.

Но именно такой способ счета применялся при счете "числами-совокупностями". Так, йорубы (одно из африканских племен), считая раковины-каури (игравшие у них роль денег), раскладывали их в кучки по 20 раковин в каждой, затем 20 таких кучек они объединяли в одну большую кучу и т. д. При таком способе счета подчеркивается то обстоятельство, что с кучами можно поступать так же, как и с отдельными раковинами. Н. Н. Миклухо-Маклай рассказывал о способе счета у папуасов, который уже очень близок к построению чисел по принципу умножения. Чтобы сосчитать число дней до возвращения корвета "Витязь", папуасы поступали следующим образом: "Первый, раскладывая кусочки бумаги на колене, при каждом обрезке повторял "каре-каре" (один), другой повторял слово "каре" и загибал при этом палец прежде на одной, затем на другой руке. Сосчитав до десяти и согнув пальцы обеих рук, он опустил оба кулака на колени, повторив "две руки", причем третий папуас загнул один палец руки. Со вторым десятком было сделано то же, причем третий папуас загнул второй палец; то же самое было сделано для третьего десятка".

Рассказывают, что так же считали стада в Южной Африке: один из африканцев считал каждую голову, второй - число десятков, сосчитанных первым, а третий - число десятков, сосчитанных вторым, т. е. число сотен. Если бы мы теперь обозначили палец первого через I, палец второго через X и палец третьего через С, то результат по мультипликативной системе записали бы, например, так: 3C2X3I. В Китае и Индии с древнейших времен существовал именно такой способ записи чисел. Кроме того, индийцы издавна проявляли глубокий интерес к большим числам и способам их записи. В одной из индийских книг - "Лалитавистаре" говорится о состязании между женихами прекрасной Гопы. Предметом состязания были письменность, арифметика, борьба и стрельба из лука. Почти половина книги посвящена описанию состязаний по арифметике. Победитель Гаутама придумал шкалу чисел, идущих в геометрической прогрессии со знаменателем 100, последним членом ее было 10^7+9*46

Следующей ступенью к позиционному принципу было опускание названий разрядов при письме (подобно тому как мы говорим "три двадцать", а не "три рубля двадцать копеек"). Но при записи больших чисел по системе с основанием 10 очень часто бывал необходим символ для обозначения нуля.

Как же появился нуль?

Мы видели, что уже вавилоняне употребляли меж-разрядовый знак. Начиная со II в. до н. э. греческие ученые познакомились с многовековыми астрономическими наблюдениями вавилонян. Вместе с их вычислительными таблицами они переняли и вавилонскую шестидесятеричную систему счисления, но только числа от 1 до 59 записывали не с помощью клиньев, а в своей, алфавитной нумерации. Но самое замечательное было то, что для обозначения пропущенного шестидесятеричного разряда греческие астрономы начали употреблять символ. Этот знак, по-видимому, и был прообразом нашего нуля.

Действительно, индийцы, владевшие уже мультипликативным принципом записи чисел, как раз между II и VI вв. н. э. познакомились с греческой астрономией. Это видно из того, что они переняли и общие теоретические положения этой астрономии, и многие греческие термины.

Одновременно они должны были познакомиться с шестидесятеричной нумерацией и греческим круглым нулем. Индийцы и соединили принципы нумерации греческих астрономов со своей десятичной мультипликативной системой. Это и был завершающий шаг в создании нашей нумерации.

Из Индии новая система распространилась по всему миру. При этом одни народы переняли у индийцев только принцип обозначения чисел, другие заимствовали и написание цифр.

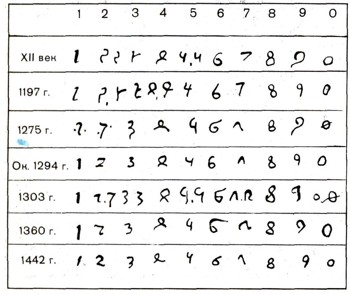
Из приведенной таблицы видно, как постепенно видоизменялись цифры "губар", употреблявшиеся в мавританских государствах. Откуда произошли сами цифры "губар", до сих пор остается неясным.

В страны Европы новая индийская нумерация была занесена арабами в X-XIII вв. (отсюда и название "арабские цифры"), однако вплоть до XVIII в. в официальных бумагах разрешалось применять только римские цифры. Но преимущества позиционного принципа счисления были настолько велики, что еще в XIII в. он стал применяться итальянскими купцами. Тогда же Леонардо Ливанский выступил убежденным сторонником новой системы. В Германии, Франции и Англии до конца XV в. новая нумерация почти не употреблялась. Но к концу XVI -началу XVII в. позиционная система одержала решительную победу - ее приняли не только купцы, но и все ученые. Ее стали применять повсеместно.

В России, как мы уже знаем, в старину употреблялась алфавитная система, которая имеет много преимуществ по сравнению с римской. Но и здесь новая нумерация быстро вошла в употребление: во всех без исключения математических рукописях XVII в. применялась десятичная позиционная система счисления. При Петре I индийские цифры уже вытесняют на монетах славянские, а позднее славянские цифры вообще быстро исчезают из обихода.

Приведем в заключение слова знаменитого французского математика и физика XVIII-XIX вв. П. Лапласа: "Мысль выражать все числа девятью знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна. Как нелегко было прийти к этому методу, мы видим на примере величайших гениев греческой учености Архимеда и Аполлония, от которых эта мысль осталась скрытой".

перейти к началу страницы