Математика

Содержание раздела

ЧИСЛА И ФИГУРЫ

Алфавитные нумерации. "Псаммит"

Мы видели, что непозиционные нумерации малоудобны: запись чисел в них очень длинна, арифметические операции производить трудно. По мере развития торговли и ремесла эти неудобства становились все чувствительнее, и вот в Малой Азии, где были древнегреческие колонии, которые вели оживленную торговлю, в середине V в. до н. э. появилась система счисления нового типа - так называемая алфавитная нумерация. Ее обычно называют ионийской. В этой системе числа обозначались при помощи букв алфавита, над которыми ставились черточки: первые девять букв обозначали числа от 1 до 9, следующие девять - числа 10, 20, 30, ..., 90, и следующие девять - числа 100, 200, ..., 900. Таким образом можно было обозначать любое число до 999.

Для обозначения чисел 1000, 2000, ..., 9000 греки употребляли те же буквы, что и для чисел 1, 2, ..., 9, но только при их записи ставили косую черточку слева внизу. Как это делалось, видно из прилагавмого здесь рисунка. Далее, для числа 10 000 употреблялся знак М^а - это число называлось мириадой ; две мириады, т. е. 20 000, обозначались так: М^бета. Этим способом можно было обозначить все числа до мириады мириад, т. е. до 10⁸. Более высокие десятичные разряды уже не могли быть записаны в ионийской нумерации и не имели названия в древнегреческом языке.

Великий математик, механик и инженер древности Архимед (III в. до н. э.) посвятил целое сочинение тому, чтобы дать общий прием наименования сколь угодно больших чисел. Издавна у греков, как, впрочем, и у других народов, наглядным образом для представления об очень большом и даже неисчислимом количестве служило число песчинок. В народных сказках, например, встречается "неразрешимая" задача: сосчитать звезды на небе, капли в море или песчинки на земле. Архимед показал, что такие задачи можно решить. Свое сочинение он так и назвал "Исчисление песка" ("Псаммит"). В нем он построил систему счета, в которой имелись числа, не только превосходящие количество песчинок в его родной Сицилии, но и такие, которые больше числа песчинок во Вселенной, если даже считать, что Вселенная сплошь заполнена песком. Но что же понимали греки времен Архимеда под всей Вселенной? В своем сочинении Архимед, следуя за греческим астрономом Аристархом Самосским, полагал, что в центре Вселенной находится Солнце, а Земля и другие планеты вращаются вокруг него. Вселенная имеет форму сферы, на поверхности которой расположены неподвижные звезды. Это была первая гелиоцентрическая система мира.

Для подсчета количества песчинок Архимед должен был, хотя бы приблизительно, определить размеры диаметров Вселенной и песчинки, а затем найти отношение их объемов. Архимед сделал это, опираясь на данные астрономии своего времени и на собственные исследования в этой области. Число песчинок, которое должно было у него при этом получиться, в нашей нумерации записывается так: 10⁶³. Это очень большое число, и до Архимеда не было средств ни для записи, ни для наименования чисел такого порядка.

Чтобы решить поставленную задачу, Архимед поступает следующим образом: все числа, меньшие мириады мириад, т. е. все числа от 1 до 10⁸ - 1, он объединяет в первую октаду (т. е. восьмерицу) и называет их первыми числами. Число 10⁸ служит единицей второй октады, в которую входят все числа от 10⁸ до 10^2*8 - 1. Это "вторые числа". Аналогично этому число 10^2*8 является единицей третьей октады, а числа от 10^2*8 до 10^3*8-1 являются "третьими". Продолжая это построение, можно дойти до мириа-до-мириадной октады, ^{которая} содержит числа от 10(в степени(10⁸-1)*8) до 10(в степени 8*10⁸)-1 Вce эти октады Архимед объединяет в первый период. Число 10 (в степени 8*10⁸) служит единицей первой октады второго периода и т. д. Этим способом можно дойти до последнего числа последней октады мириадо-мириадного периода. Здесь Архимед останавливается, но ясно, что можно идти дальше, объединив все периоды в новый разряд.

Но и тех чисел, которые построил Архимед, вполне достаточно для подсчета числа песчинок во Вселенной. Необходимое число содержится уже в восьмой октаде первого периода. Архимед продолжил свое построение дальше для того, чтобы разъяснить метод наименования сколь угодно больших чисел.

Для построения своих чисел Архимед формулирует правило, равносильное нашей формуле:

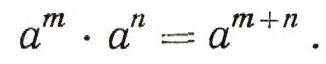
Способ Архимеда близок к позиционному, но понадобилось еще около тысячи лет, прежде чем человечеству удалось создать десятичную позиционную систему счисления.

Алфавитные системы были кроме ионийцев у древних евреев, финикийцев, армян, грузин и других народов. Алфавитная нумерация была принята и в Древней Руси. Над буквами, обозначающими числа, ставился специальный знак - титло. Это делалось для того, чтобы отличать их от обычных слов.

Интересно отметить, что хотя в славянской нумерации, как и в греческой, запись числа шла слева направо, от высших единиц к низшим, но для чисел от 11 до 19 делалось исключение: сначала писали единицы, а затем знак для 10.

Удобны ли алфавитные системы? Запишем в славянской нумерации число 444:

Мы видим, что запись получилась не длиннее нашей. Это объясняется тем, что в алфавитных нумерациях имелось 27 цифр, тогда как в египетской, например, для обозначения всех чисел до 1000 было всего лишь три цифры.

Но алфавитные нумерации имели и крупный недостаток: с их помощью нельзя обозначать сколь угодно большие числа. Они были удобны только для зариси чисел до 1000.

Правда, славяне, как и греки, умели записывать и большие числа, но для этого к алфавитной системе добавляли новые обозначения. Числа 1000, 2000 и т. д. они записывали теми же буквами, что 1, 2 и т. д., только слева внизу ставился специальный знак

например 1000 обозначали:

 

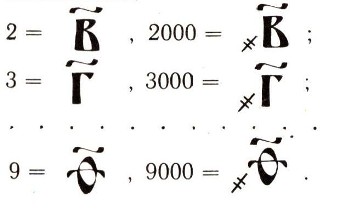
Число 10 000 опять обозначалось той же буквой, что и 1, только без титла, но его уже обводили кружком: 10000 =

Называлось это число "тьмой". Отсюда, между прочим, произошло выражение "тьма народу". Итак, для обозначения тем первые 9 цифр обводились кружками:

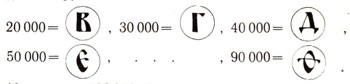
10 тем, или 100000, было единицей высшего разряда. Ее называли "легион". В записи вокруг первых 9 цифр ставился кружок из точек:

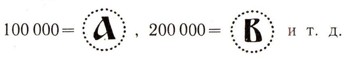
10 легионов составляли новую единицу, которая называлась "леодр". Для обозначения леодров соответствующие числа заключали в кружок из черточек:

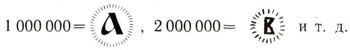
Эти обозначения можно рассматривать как зачатки позиционной системы, так как в ней для обозначения единиц разных разрядов применялись одни и те же символы, к которым добавлялись знаки для определения разряда. Такая система называлась малым числом. В ней обозначения не шли дальше миллионов.

Но наряду с этим имелось и "большое", или "великое", число, в котором словом "тьма" обозначался уже миллион. Тьма тем (т. е. 10¹²) называлась легионом, легион легионов (т. е. 10²⁴) - леодром, леодр леодров (т. е. 10⁴⁸) - "вороном", и, наконец, число 10⁴⁹ называлось "колодой". В рукописи XVII в. говорится: "И более сего несть человеческому уму разумевати", т. е. для больших чисел уже нет названий. Для обозначения воронов буквы ставили в кружок из крестиков :

а колоду обозначали так:

Алфавитные нумерации, как мы говорили, были мало пригодны для оперирования с большими числами, встречавшимися уже в древности (например, при астрономических расчетах). В ходе развития человеческого общества эти системы уступили место позиционным. Но остатки алфавитных нумераций сохранились в нашем обиходе и по сей день. Так, мы часто нумеруем пункты при помощи букв алфавита. Правда, буквы служат только для обозначения последовательного порядка, а не количества. Никаких арифметических операций над такими буквами мы уже не производим.

перейти к началу страницы