Преобразования подобия

Преобразования, сохраняющие форму фигур, но, возможно, изменяющие их размеры, называются преобразованиями подобия. Каждую фигуру F преобразование подобия переводит в подобную ей фигуру F', представляющую собой увеличенную или уменьшенную копию первоначальной фигуры; все размеры фигуры F' равны соответствующим размерам фигуры F, умноженным на одно и то же число k (рис. 15,16). Это число называется коэффициентом подобия двух фигур.

Рис 15. Подобные фигуры.

Рис. 16. Подобные фигуры.

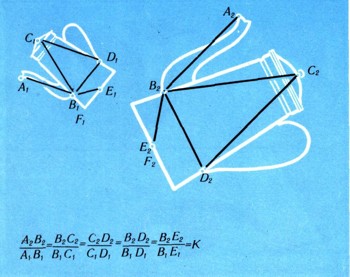
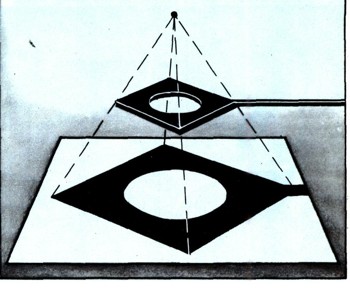
Подобные фигуры можно получить, например, поместив под лампой вырезанную из куска картона фигуру F, плоскость которой параллельна поверхности стола; в таком случае тень F', отбрасываемая этой фигурой на стол, будет подобна фигуре F (рис. 17).

Рис. 17 Подобные фигуры можно получить и так.

Более "математический" пример преобразования подобия представляет собой гомотетия с центром О и коэффициентом k, переводящая каждую точку А в такую точку А' луча ОА, что ОА'/ОА = k'(рис. 18).

Рис. 18 Гомотетия с центром О.

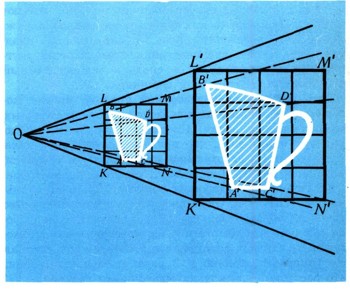
Некоторые свойства фигуры F', подобной фигуре F, будут отличаться от свойств фигуры F; так, например, гомотетия с коэффициентом 2 переводит фигуру ABDC в фигуру A'B'D'C', площадь которой в 4 раза больше площади фигуры ABDC (рис. 18). Но большинство свойств фигуры F' будет совпадать со свойствами фигуры F: так, все имеющиеся на фигуре F' углы будут равны соответствующим им углам, имеющимся на фигуре F; отношение расстояний между какими-либо точками фигуры F' будет равно отношению расстояний между соответственными точками фигуры F (скажем, АВ/CD=А'В'/C'D') и т.д.)

Рис. 19.

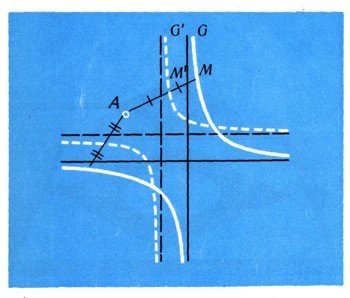
Таким образом, преобразования подобия меняют свойства геометрических фигур очень мало: окружность они переводят снова в окружность, квадрат - в квадрат, равнобедренный треугольник с углом при вершине в 40° - снова в равнобедренный треугольник с углом при вершине в 40°.

Эти свойства преобразований подобия иногда могут быть использованы для решения содержательных геометрических задач. Поставим, например, такую задачу: определить, что представляет собой множество середин всех отрезков AM, где точка А фиксирована, а точка М пробегает, скажем, равностороннюю гиперболу G (график обратной пропорциональной зависимости). Очевидно, что искомое множество точек М' образует фигуру G', гомотетичную гиперболе G с центром гомотетии А и коэффициентом гомотетии 1/2. Отсюда следует, что это будет точно такая же гипербола, только в 2 раза "меньшая" (такая, что, расстояние между двумя точками гиперболы G' в 2 раза меньше расстояния между соответствующими точками гиперболы G; рис. 19).

перейти к началу страницы