Задача о взвешивании

Вот одна из классических задач, решить которую можно сразу же, если выбрать систему счисления с подходящим основанием. Эта задача приведена в математической книге знаменитого математика XIII в. Леонардо Пизанского. Ею интересовался также в XVIII в. и Л. Эйлер.

Требуется выбрать 5 гирь так, чтобы с их помощью можно было взвесить (с точностью до 1 кг) любой груз до 30 кг при условии, что гири ставятся только на одну чашу весов и масса гирь различна. Какие же гири нужно выбрать?

Сумма масс всех гирь должна быть не меньше 30 кг. Но, конечно, этого недостаточно. Если мы выберем, например, гири в 1, 2, 3, 10и 15 кг, то с их помощью нельзя будет взвесить грузы в 7, 8, 9, 22, 23 и 24 кг.

Разберем математический смысл задачи. Чтобы взвесить' некоторый груз, помещая гири только на одну чашу весов, надо представить его массу в виде суммы масс имеющихся гирь, причем так, чтобы каждая гиря бралась не более одного раза. Если выбранные нами гири имеют массу т₁, т₂, m₃, т₄, т₅, то груз массой М=<30 кг должен представляться так:

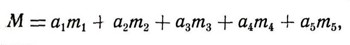
где каждый коэффициент равен единице, если кладем соответствующую гирю на чашу весов, и нулю, если не пользуемся ею при взвешивании.

При такой постановке вопроса видно сходство с представлением числа М в двоичной системе счисления. Нужно только в качестве т₁, т₂, т₃, m₄, m₅

взять гири массой: т₁ = 1 кг, m₂=2 кг, m₃ = 4 кг, m₄ = 8 кг, m₅ = 16 кг. Сумма их масс 1 + 2 + 4,+ 8 + 16 = 31 кг. Кроме того, каждое число М, не большее 31, можно представить в виде:

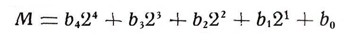
где каждый из коэффициентов b₀, b₁, b₂, b₃, b₄ будет, как нам и нужно, либо нулем, либо единицей.

Пусть, например, надо взвесить груз в 22 кг. Запишем число 22 по двоичной системе: 22=10110₂.

Значит, нужно взять гири m₂ = 2 кг, m₃ = 4 кг и m₅ = 16 кг.

Теперь несколько видоизменим задачу: пусть требуется выбрать 4 гири, с помощью которых можно было бы взвесить любой груз до 40 кг, при условии, что гири можно класть и на левую и на правую чашу весов.

Нетрудно убедиться, что для решения этой задачи можно воспользоваться троичной системой счисления, выбрав следующие 4 гири: m₁ - 1 кг, m₂ = 3 кг, m₃ = 9 кг, m₄ = 27 кг. Нужно только заметить, что двойной вес гирь т₁, m₂, m₃ можно заменять разностью двух разных гирь, например: 2m₂ = m₃ - m₂, m₃ = m₄ - т₃ и т. п.

Следует помнить, что, хотя в различных системах счисления числа записываются по-разному, основные свойства их от этого не меняются: так, число 20 будет делиться на 2, в какой бы системе мы его ни записали, а 27 не разделится на 2, но будет делиться на 3. Числа 3, 5, 7 останутся простыми в любых системах счисления. Однако признаки делимости, которые устанавливаются исходя из записи числа в определенной системе счисления, будут меняться вместе с основанием системы. Так, число делится на 5, если его запись в десятичной позиционной системе оканчивается нулем или пятеркой. Но число не всегда делится на 5, если на 0 оканчивается его запись в троичной системе, например, числа 10₃(т. е. 3), 100₃ (т. е. 9), 1000₃ (т. е. 27) не делятся на 5, а число 120₃ (т. е. 15) будет делиться на 5.

перейти к началу страницы