Движения

Приведем примеры движений плоских фигур. Параллельным переносом называется движение, при котором фигуру как целое перемещают в определенном направлении, не поворачивая ее.

Рис. 5 Параллельный перенос.

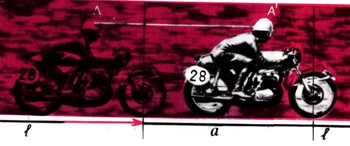
Параллельный перенос характеризуется направлением, которое задается указанием некоторой прямой l с поставленной на этой прямой стрелкой и расстоянием а, на которое переносятся фигуры. Каждую точку А параллельный перенос переводит в такую точку А', что АА'||l (причем направление от точки Л к точке А' совпадает с тем, которое указано стрелкой на прямой l) и А А' =а (рис. 5).

Рис. 6 Поворот вокруг точки О на угол а.

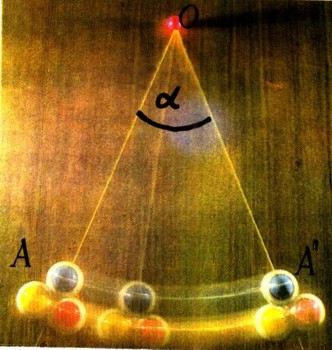
Поворот вокруг точки О на угол а характеризуется тем, что каждая точка А переходит в такую точку А'', что ОА = ОА' и угол AOA' = a (рис. 6); при этом должно быть указано также и направление поворота, которое может совпадать с направлением вращения часовой стрелки или быть противоположно ему. Поворот вокруг точки О на угол 180° называется также симметрией относительно точки О; здесь каждая точка А переходит в такую точку А', что О есть середина отрезка АА' (рис. 7).

Рис. 8 Симметрия относительно прямой l.

Еще один важный пример движения представляет собой симметрия относительно прямой l; это движение можно реализовать, перегнув лист бумаги по прямой l. Симметрия относительно прямой l переводит каждую точку А в такую точку А', что отрезок АА' перпендикулярен прямой l и делится этой прямой пополам (рис. 8). Каждый легко может получить симметричные фигуры, сделав кляксу на листе бумаги и затем перегнув лист (рис. 9).

Рис. 9 Симметричные фигуры.

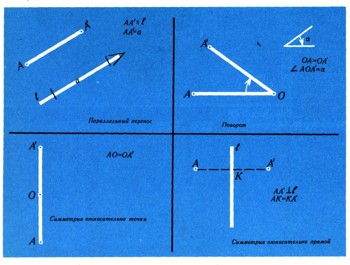
Эти примеры достаточно хорошо характеризуют содержание понятия "движение". Каждое движение задается указанием определенного закона или правила, указывающего, как найти точку А', в которую это движение переводит произвольную точку А. На рис. 10 перечислены правила, относящиеся к указанным выше движениям. Вообще, задание правила, позволяющего перейти от произвольной точки А к новой точке А' (которая может и совпадать с исходной точкой А), определяет геометрическое преобразование.

Рис. 10. Правила, по которым точка А переводится в точку А'.

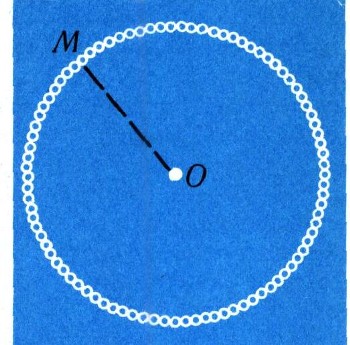
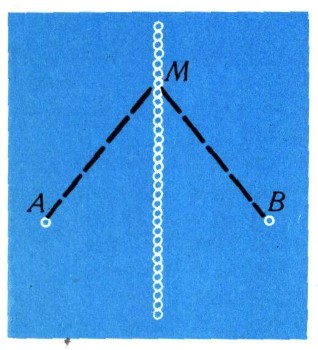
Под фигурой в геометрии понимают совокупность (или множество) точек; так, окружность с центром О и радиусом r есть совокупность таких точек М, что ОМ = r (рис. 11); отрезок с концами А и В есть совокупность таких точек М, что AM + MB =AB (рис. 12); прямую можно охарактеризовать как совокупность таких точек М, что АМ = ВМ, где точки А и В заданы (рис. 13).

Рис. 11

Рис. 12

Рис. 13

Геометрическое преобразование переводит каждую точку А, входящую в состав фигуры F, в новую точку А'. При этом совокупность точек фигуры F переходит в некоторую новую совокупность точек, образующую фигуру F'. Про фигуру F' говорят, что она получается рассматриваемым преобразованием из фигуры F (рис. 14).

Рис. 14

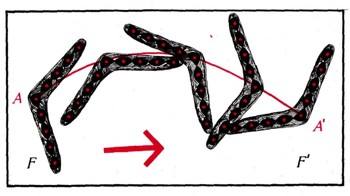
Движения представляют собой простейшие геометрические преобразования - такие, которые переводят каждую фигуру F в равную ей фигуру F', т. е. сохраняют форму и размеры фигур. Можно определить движения как геометрические преобразования, сохраняющие расстояния между точками: если точки А и В движение переводит в точки А' и В', то А'B' = АВ.

перейти к началу страницы