Математика

Содержание раздела

ЧИСЛА И ФИГУРЫ

Счет двойками, тройками и дюжинами

Однако вовсе не обязательно считать десятками. Можно, например, вести счет двойками или тройками. Для этого за основание системы счисления примем число 2 или 3, а в остальном будем поступать точно так же, как это делали, когда основание равнялось десяти. Для записи по двоичной системе понадобятся всего две цифры: 0 и 1. Число "два" в этой системе запишется как 10, так как 2=1*2 + 0. А чтобы не спутать нашу запись с обычной, будем справа внизу ставить маленькую цифру 2 - это будет означать, что основанием системы служит число "два". Итак, 10₂ будет записью числа 2, 11₂-записью числа 3, так как 3 = 1-2 + 1.

Число 4=1-2²+0-2 + 0-1, поэтому оно запишется в виде 100₂. Записью числа 5 будет 101₂, число 7 будет выглядеть так: 111₂ Чтобы найти запись любого натурального числа N, нужно определить остатки от последовательного деления этого числа на 2. Мы предоставляем читателям проверить, что записью числа 35 в двоичной системе будет 100011₂. Если число N таково, что

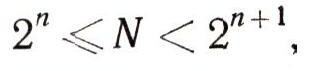
то его можно представить в виде:

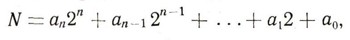
т, е. это число в двоичной системе запишется так:

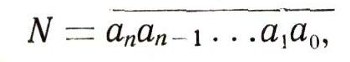
но здесь уже каждый из коэффициентов а_i может принимать только одно из двух значений: 0 или 1.

Более подробно о двоичной системе, которая сейчас приобрела большое значение в связи с ее применением в быстродействующих вычислительных машинах, узнаете, если прочтете статью "Электронные вычислительные машины", помещенную в этом томе.

Для записи числа в троичной системе нужны три цифры, например 0, 1, 2. Число 3 здесь будет записываться как 10₃, а 4- как 11₃. Записью числа 35 в этой системе является 1022₃.

Но можно считать и дюжинами, т. е. пользоваться системой счисления с основанием двенадцать. Еще не так давно в нашей стране и в Западной Европе некоторые предметы, например перья и карандаши, принято было считать дюжинами. Сервизы тоже обычно составляют из 12 чашек, 12 блюдец, 12 тарелок, а комплекты мебели - из 12 стульев или кресел. Существовало даже специальное название для дюжины дюжин - гросс.

О широком распространении двенадцатеричной системы свидетельствуют такие факты: мы до сих пор делим год на 12 месяцев, а сутки на 24 часа, прячем в повседневной жизни часы считаем только до 12, а затем начинаем счет сначала ("час дня", "два часа дня" и т. д.). Число 12 часто встречается также в сказках и легендах (двенадцатиглавый змей, двенадцать братьев-разбойников), что свидетельствует о древнем происхождении двенадцатеричной системы счисления. Посмотрим, как будут изображаться числа в этой системе.

Во-первых, в ней должно быть двенадцать цифр. Значит, к нашим десяти цифрам надо прибавить еще две, например А для обозначения десяти и Б -для одиннадцати. Во-вторых, запись чисел в ней будет короче, чем в нашей системе, а таблица умножения длиннее. Число 12 запишется как 10₁₂ (снова ставим значок 12 для того, чтобы знать, в какой системе сделана запись), число 13 - как 11₂, число 35 = 2*12 + 11 - как 2Б₁₂, а число 133 = 11 * 12 + 1 -как Б1₁₂, т. е. оно станет двузначным.

Ниже мы расскажем о том, что когда-то существовали нумерации с основанием 20 и даже 60. А теперь сделаем некоторые общие выводы: 1) всякое натуральное число, отличное от единицы, может служить основанием позиционной системы счисления; 2) в системе счисления должно быть столько цифр, сколько единиц содержится в основании системы.

Несмотря на то что принципиально все позиционные системы счисления равноправны, некоторыми из них в определенных случаях пользоваться особенно удобно. Например, как мы уже говорили, при счете на электронных вычислительных машинах в основном пользуются двоичной системой.

Приведем несколько задач, для решения которых удобнее воспользоваться не десятичной, а другими системами счисления.

перейти к началу страницы