Математика

Содержание раздела

ЧИСЛА И ФИГУРЫ

Как люди считали в старину и как писали цифры

Все числа мы привыкли записывать с помощью десяти знаков - цифр: О, 1, 2, 3, 4, 5, 6, 7, 8, 9. Например, число, состоящее из четырех сотен, четырех десятков и четырех единиц, мы записываем так: 444. При этом один и тот же знак "4" обозначает число единиц, если он стоит на последнем месте, число десятков - если на предпоследнем, и число десятков десятков, т. е. сотен, если он стоит на третьем месте от конца. Такой принцип записи чисел называется позиционным, или поместным, потому что каждая цифра получает числовое значение не только в зависимости от своего начертания, но и от того, на каком месте она стоит при записи числа. Позиционный принцип позволяет с помощью десяти знаков -цифр записать любое сколь угодно большое число. Действительно, пусть нам дано натуральное число N. Для того чтобы записать его в нашей системе, находим сначала остаток от деления N на 10, затем остаток от деления частного на 10 и т. д. - до тех пор, пока в качестве частного не получим число, меньшее 10. Например:

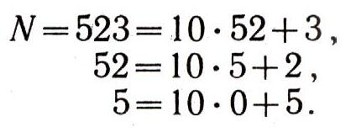
Полученные остатки и являются последовательными цифрами нашего числа, записанного в позиционной десятичной системе:

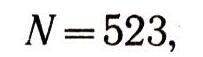
или, более подробно:

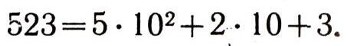
Для тех, кто знаком с алгеброй, скажем, что каждое натуральное число М можно представить в таком же виде.

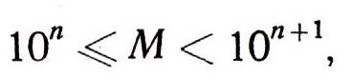
то

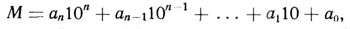
где каждый из коэффициентов a₀, а₁, ..., а_n меньше 10 (это просто остатки от последовательного деления числа М на 10). Следовательно, каждый из коэффициентов выразится одной из десяти цифр. Следуя десятичному позиционному принципу, записываем число М так:

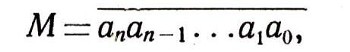
где а₀ означает число обычных единиц, или единиц первого разряда, содержащихся в М; а₁ - число единиц второго разряда, т. е. десятков; a₂ - число единиц третьего разряда, т. е. сотен, и т. д. (Чтобы запись не воспринималась как произведение а_n*a_n-1...*а₁* a₀, сверху ставится черта.)

Число 10 называется основанием нашей системы. Итак, для записи чисел мы пользуемся десятичной позиционной системой счисления.

перейти к началу страницы