Что такое геометрия

Прежде чем завести разговор о геометрических преобразованиях, остановимся на вопросе о самом содержании предмета геометрии. Впоследствии мы увидим, что к понятию геометрического преобразования этот вопрос имеет самое непосредственное отношение.

Рис. 1

Рис. 2

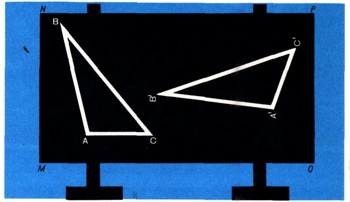
Геометрия изучает свойства плоских фигур и пространственных тел. Однако в геометрии рассматриваются вовсе не все свойства фигур или тел. Ясно, например, что цвет или вес тела для геометра безразличен - геометрические свойства куба останутся одними и теми же независимо от того, идет ли речь о металлическом кубе или о кубе, сделанном из фанеры и окрашенном в красный цвет. (Заметим, что физические свойства этих двух кубов во многом будут различны.) Так же и расстояние от вершины изображенного на доске треугольника до края доски не интересует геометра. Один из двух равных между собой треугольников (рис. 1) расположен заметно ближе к краю MN доски, чем второй; однако все геометрические свойства этих треугольников -длины их соответственных сторон, величины углов, высоты, медианы, площади, радиусы вписанной и описанной окружностей, расстояние от центра описанной окружности до точки пересечения медиан и т. д. - будут одинаковыми. Как же охарактеризовать тот круг свойств фигур и тел, который интересует геометра?

Рис. 3

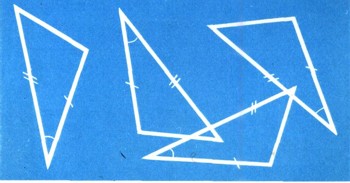
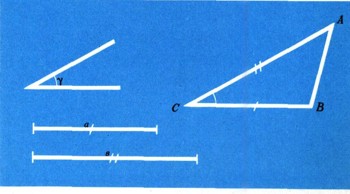
Все свойства тел, которые рассматриваются в геометрии, полностью определяются формой и размерами тела и никак не зависят от его расположения. Другими словами, это означает, что каждые две равные фигуры или два равных тела обладают в точности теми же самыми геометрическими свойствами; поэтому геометр не может иметь никаких оснований для того, чтобы как-либо различать эти фигуры или тела. Это обстоятельство подразумевается и в самом названии "равные тела". Так, например, говорят, что задача построения треугольника ABC no двум сторонам ВС = а и АС - b и углу ACB=y имеет единственное решение (рис. 2). На самом деле существует, конечно, очень много (даже бесконечно много!) треугольников, имеющих две стороны длин а и b и заключенный между ними угол величины y (рис. 3). Однако все эти треугольники равны между собой, поэтому мы их принимаем за один треугольник.

Рис. 4

Вспомним теперь, какие фигуры или тела считаются в геометрии равными. Две фигуры F и F' (рис. 4) называются равными (или конгруэнтными), если при наложении одной из них на другую они совпадают всеми своими точками, другими словами - если существует движение, при помощи которого можно совместить фигуру F с фигурой F'. Таким образом, само определение равенства фигур (или тел) связано с понятием движения. Учитывая определение равенства фигур, мы можем сказать, что фигуры, получающиеся одна из другой движением, считаются в геометрии одинаковыми, не различаются между собой; все геометрические свойства одной из этих фигур совпадают с геометрическими свойствами другой фигуры. Последнее обстоятельство можно принять за предварительное определение геометрических свойств, т. е. тех свойств фигур и тел, которые изучаются геометрией: геометрия изучает свойства фигур и тел, которые сохраняются при движениях.

перейти к началу страницы