Краткие сообщения. Теоретическое описание гранулированых материалов

Гранулированные (то есть, сыпучие) материалы (granular materials) уже давным давно используются человеком в быту, в промышленности, в технологии. Примером может служить обыкновенный песок с его многообразием применений. И что поразительно, несмотря на огромное прикладное значение свойства гранулированных материалов до недавнего времени практически не изучались.

Лет 10-15 назад физики "вдруг" осознали, что обыкновенный песок является совершенно поразительным материалом. При соответствующих условиях он может вести себя и как твердое тело, и как жидкость, и как газ. Причем каждая "фаза" обладает уникальными свойствами, отличающими гранулированные материалы от всех других веществ. Не в силах рассказать здесь обо всех особенностях поведения гранулированных материалов, мы отсылаем читателя к вводному обзору [1] и веб-странице [2]. Здесь же мы остановимся на одном очень интересном аспекте этого поведения: фазе "гранулированной жидкости" и попытках ее теоретического описания.

Представьте себе, что у вас есть контейнер с песком, который мелко дрожит, трясется. Энергия этого движения передается и отдельным песчинкам. В результате при достаточно сильном дрожании наступает фазовый переход: вся масса гранулированного материала приходит в движение, начинает течь, ведет себя как некая "гранулированная жидкость".

Чем же она отличается от обычной жидкости? Отличие одно, но важное: взаимодействия песчинок очень непохоже на взаимодействие молекул. А именно,

между песчинками нет сил притяжения,
столкновения песчинок неупруги,
между песчинками существует трение.

Оказывается, это кардинально меняет дело и приводит к возникновению двух связанный друг с другом явлений: неустойчивости относительно кластеризации и спонтанного рождения вихрей.

Первое явление означает, что в системе возникают неоднородности плотности, которые не исчезают, а наоборот -- усиливаются, что приводит к распаду жидкости на отдельные кластеры. Причина довольно проста: если в какой-то области увеличилась концентрация частиц, то это приводит к увеличению числа столкновений, что в силу их неупругости приводит к падению скорости частиц относительно окружения. Это значит, что в этом районе нарушится баланс потоков: частиц, влетающих в этот объем, будет больше, чем вылетающих. А это приводит к дальнейшему увеличению локальной плотности: неоднородность растет. На Рисунке 1 показано несколько последовательных стадий эволюции свободно "остывающего" гранулированного материала. Ясно видно возникновение кластеров и их развитие (иллюстрация взята из работы [3]).

Рис.1 Последовательные этапы кластеризации в гранулированных материалах

В частности, если на систему не действует сила тяжести, то в случае очень неупругих соударений возникает так называемый "неупругий коллапс", когда когда за конечное время происходит бесконечное число столкновений, и движение частиц абсолютно замирает (см. Java-апплет на сайте [4] -- впечатляющая иллюстрация).

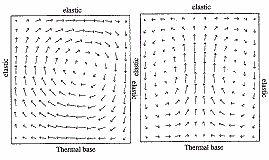
Рис.2 Конвекция в гранулированных материалах

Если же жидкость находится в поле тяжести, то области с повышенной плотностью будут, раумеется, тяжелее окружающей жидкости. В результате возникнет гидродинамическая неустойчивость, начнется конвекция, спонтанно появятся вихри. Это и есть второе указанное явление. На Рисунке 2 показаны типичные конвекционные режимы в гранулированных материалах.

Итак, явления существуют, и потому возникает закономерный вопрос: как они могут быть теоретически выведены из микроскопической динамики отдельных песчинок? Построена ли теория, описывающая и объясняющая поведение гранулированных материалов?

Оказывается, нет. Несмотря на то, что в последнее десятилетие появилось огромное количество работ, посвященных физике гранулированных материалов, их подавляющее большинство -- это компьютерное моделирование явления, не более того. Настоящее же теоретическое описание поведения гранулированных материалов, как это не парадоксально, находится пока в зачаточном состоянии. Оказывается, что отличия гранулированных материалов от обычных веществ не только приводит к новым интересным явлениям, но и значительно усложняют их описание.

Стандартный подход к теоретическому описанию гранулированных жидкостей заключается в следующем. Берутся уравнения обычной гидродинамики и адаптируются с учетом специфики гранулированных материалов. А именно, вначале выбирается такое уравнение состояния гранулированной жидкости, которое могло бы приводить к кластеризации (то есть, локальная температура должна падать при повышении плотности). Далее, вводится дополнительный член, описывающий диссипацию энергии из-за неупругого столкновения частиц. Наконец, выбирается некая реологическая модель материала (модель, описывающая вязкоупругие свойства, то есть, то, как материал деформируется и течет под действием напряжений), а также фиксируется зависимость коэффициента теплопроводности от параметров гранулированной жидкости. После этого можно пытаться решить полученные уравнения и выводить из них наблюдаемые эффекты.

В той или иной степени прогресс в этом направлении имеется. Например, в работе [5] на основании таких уравнений теоретически исследовалась текучесть гранулированной жидкости, заключенной между двумя вращающимися соосными цилиндрами. Несмотря на то, что уравнения базировались на упрощенной модели межчастичного взаимодействия, была обнаружена очень нетривиальная зависимость текучести материала от средней плотности и от температуры. В частности, было отмечено аномально быстрое увеличения коэффициента вязкости с ростом плотности (точнее, при приближении плотности к критическому значению, за которым материал перестает течь). Кроме того, несмотря на то, что выбранная модель чисто гидродинамическая, авторы смогли проследить, как происходит "затвердевание" гранулированной жидкости, то есть, как вязкое поведение сменяется упругим.

Несколько иной подход к проблеме состоит в попытке описать поведение гранулированных жидкостей нелинейными гидродинамическими уравнениями типа уравнения Бюргерса. Идея эта берет свое начало в работах Шандарина и Зельдовича [6], где уравнение Бюргерса использовалось для описания одномерного газа с абсолютно неупругими столкновениями частиц. Оказывается, что и в случае частично-упругих столкновений эволюция гранулированной жидкости при больших временах также походит на динамику решений уравнения Бюргерса, см. работу [7]. По крайней мере было отмечено формирование фронтов ударных волн (т.е. кластеризация в одномерном случае), а это, как известно, очень характерно для уравнения Бюргерса.

В настоящее время, однако, совершенно неясно, насколько такой подход справедлив в многомерном случае; этот вопрос сейчас активно изучается.

Очень интересный подход к описанию макроскопических явлений в гранулированной жидкости был использован в недавней работе [8]. В ней исследовались нелинейные гидродинамические уравнения в достаточно общем виде, без выбора конкретной модели для той или иной характеристики жидкости. Авторы показывают, что можно ввести некий параметр порядка, который определяется через поле скоростей частиц. Возникающие же уравнения можно переписать в виде уравнений на этот параметр порядка. Эти уравнения будут содержать эффективный потенциал, минимум которого и даст нам решение для параметра порядка, а значит, и решение исходной задачи об эволюции системы.

В результате вся теоретическая конструкция приобретает совершенно новый смысл: теория становится разновидностью общей теории фазовых переходов второго рода (и критических явлений вообще) Гинзбурга-Ландау. Обычно в таких теориях естественным образом возникает некая критическая точка в эволюции системы, пройдя которую, система "перестраивается", претерпевает некий топологический переход, связанный с нарушением симметрии в системе. Параметр порядка при этом принимает ненулевое значение.

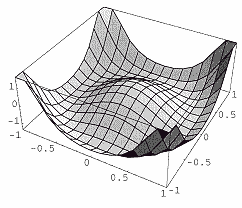
Рис.3 Форма эффективного потенциала как функции параметра порядка; минимум достигается при целом множестве отличных от нуля параметров порядка

В нашем случае такой переход со спонтанным нарушением симметрии тоже есть. Авторами показывается, что если бы эффективный потенциал имел минимум при нулевом параметре порядка, то распределение скоростей в гранулированной жидкости было бы однородно. Однако потенциал имеет вид "сомбрерро", а значит, минимум достигается при целом множестве отличных от нуля параметров порядка (Рисунок 3). В терминах поля скоростей это значит, что однородность этого поля нарушается, и в системе самопроизвольно возникают вихри.

В целом же, теория гранулированных материалов пока только делает свои первые шаги. Благодаря тому, что пока еще не выработана однозначная парадигма этого раздела теоретической физики, каждый исследователь пытается взглянуть на задачу под новым углом и разработать теорию, непохожую на методы предшественников. Такая ситуация, безусловно, очень полезна как для самой теории, так и для делающих ее людей.

Ссылки:

[1] H.Jaeger, S.Nagel, R.Behringer, Rev.Mod.Phys.68, 1259 (1996)
[2] http://www.nsu.ru/materials/ssl/text/news/Physics/050.html"
[3] S.Luding, H.Herrmann, Chaos 9, 673 (1999), http://www.haverford.edu/physics-astro/gollub/vib_granular/inelastic/inelastic.html"
[5] L.Bocquet et al, "Granular Shear Flow Dynamics and Forces: Experiment and Continuum Theory",

перейти к началу страницы