Новости науки 11.10.01. Роль "запутанности" в двухфотонной технике получения изображений.

Давно известно, что при использовании одиночных фотонов можно воспроизвести все известные классические эффекты дифракции, интерференции и получения изображений - необходимо только повторить "однофотонный" эксперимент достаточное количество раз. Однако возможно наблюдение и более необычных эффектов "двухфотонной" оптики, когда "работают" два запутанных в квантово-механическом смысле фотона: один из них проходит через оптическую систему с каким-то объектом (например, щелью), а соответствующее изображение (например, дифракционная картина) получается с помощью другого. Недавно ученые из Бостонского университета показали, что в системе двух коррелированных в классическом смысле (но не "запутанных") фотонов подобные двухфотонные изображения не могут быть получены при сколь угодно сильной корреляции.

Еще в первой половине девяностых были проведены эксперименты, демонстрирующие необычный с классической точки зрения двухфотонный эффект (когда один фотон как бы "чувствует", что происходит с другим, хотя в классическом смысле они не взаимодействуют), причина которого кроется в запутанной в квантово-механическом смысле природе двухфотонных состояний. Например, в работе [1] пара запутанных фотонов, имеющих взаимно перпендикулярные направления поляризации, разделялась с помощью поляризационного расщепителя, после чего один из фотонов проходил через щель (или систему с двумя щелями), а дифракционная (интерференционно-дифракционная) картина наблюдалась при регистрации прихода второго фотона из пары.

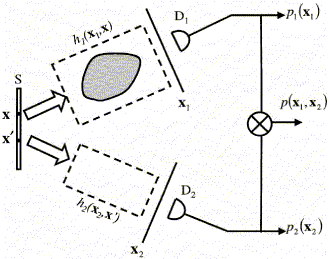
Рис.1. Схема, поясняющая двухфотонную технику получения изображений. Двухфотонный источник испускает фотоны, один из которых попадает в оптическую систему, содержащую некий объект, а второй - в другую оптическую систему. Детекторы D₁ и D₂ регистрируют приход одиночных фотонов; двухфотонное изображение (например, дифракционная картина) получается при перемещении детектора в плоскости x₂ на выходе "пустой" оптической системы, причем приход фотона фиксируется только при совпадении срабатывания двух детекторов (детектор в системе с объектом служит в качестве источника опорного сигнала).

Однако оставался невыясненным вопрос, нельзя ли, каким-либо образом оперируя с коррелированными в классическом смысле фотонами, воспроизвести подобный эффект. Теоретическая работа [2] посвящена именно этому вопросу. Ученые из Бостонского университета рассмотрели возможность получения изображений как с помощью пар "запутанных" фотонов (схема получения двухфотонных изображений показана на Рис.1), так и с использованием пар коррелированных в классическом смысле фотонов. В их работе было показано, что никакая сколь угодно сильная классическая статистическая корреляция не позволяет воспроизвести эффект, основанный на запутанности фотонов. Различие между "квантовым" и "классическим" случаем можно пояснить следующим образом. Можно рассмотреть две возможные схемы детектирования одного из фотонов пары: 1) приход одного фотона в некоторую точку на плоскости x₂ (см. рисунок) регистрируется независимо от того, был ли зафиксирован приход второго фотона; 2) приход фотона в некоторую точку на плоскости x₂ регистрируется только если зафиксирован фотон на выходе из другой оптической системы (в любой точке плоскости x₁). С точки зрения классической теории вероятности две определенные таким образом плотности вероятности регистрации фотона неразличимы, однако в случае пары запутанных фотонов плотности вероятности для двух этих случаев имеют, вообще говоря, различный вид. Поэтому только в последнем случае мы можем получать какую-то информацию об объекте, помещенном в другую оптическую систему.

1. D.V.Strekalov, A.V.Sergienko, D.N.Klyshko, and Y.H.Shyh. Phys.Rev.Lett. v.74, 3600 (1995).

2.Ayman F.Abouraddy, Bahaa E.A.Saleh, Alexander V.Sergienko, and Malvin C.Teich. Phys.Rev.Lett. v.87, 123602 (2001).

перейти к началу страницы