Новости науки 06.01.02. Экспериментальное доказательство нелокальной природы квантовой телепортации.

Одно из самых удивительных явлений, имеющих принципиально квантовомеханическую природу, - квантовая телепортация, возможность переноса квантового состояния одного объекта на другой объект. Эксперименты, проведенные в группе А.Цайлингера в Венском университете, убедительно продемонстрировали нелокальную природу квантовой телепортации.

Квантовая механика запрещает "клонирование" состояний, т.е. невозможно, получив полную информацию о квантовом объекте A (изначально его состояние неизвестно), создать второй, точно такой же, объект, не разрушив первый. Однако, как было теоретически показано в начале 90-х годов прошлого века, возможно, разрушив квантовое состояние A в одной точке пространства, создать точно такое же в другой точке; эта процедура получила название "квантовой телепортации". Квантовая телепортация была продемонстрирована на практике в 1997 г. в группе А.Цайлингера в Венском университете.

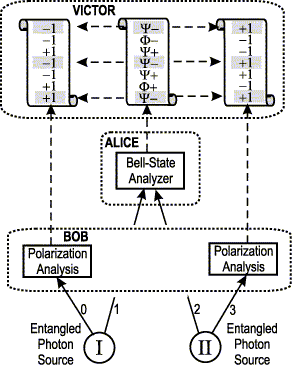
Рис.1. Логическая схема эксперимента.

Ключевую роль в квантовой телепортации играют так называемые запутанные состояния. Примером системы, находящейся в запутанном состоянии, являются два фотона, появившиеся в результате спонтанного параметрического распада фотона, распространяющегося в среде с квадратичной нелинейностью (например, в кристалле BaB₂O₄) - именно так получались пары запутанных фотонов в экспериментах, о которых речь пойдет ниже. Для запутанных фотонов нельзя указать, какова поляризация каждого из фотонов пары; если же произвести измерение над одним фотоном и - тем самым - определить его поляризацию, то и поляризация другого фотона также станет определенной. Стоит подчеркнуть, что производя измерение над одной частицей мы в тот же момент определяем и состояние другой частицы, как бы далеко эти частицы друг от друга ни находились. Таким образом, связь между частицами носит принципиально нелокальный характер. Действительно, в рамках классического подхода после того, как система распалась на составные части, никакое воздействие на одну из частей не может изменить состояние другой части, если частицы не взаимодействует. И более того, поскольку скорость распространения сигнала не может превышать скорости света, то при определенных условиях - в рамках классического подхода - воздействие на одну часть системы никаким образом не может повлиять на другую часть системы. В математическом виде это утверждение было сформулировано Дж.Беллом в 1964 г. в виде так называемых неравенств Белла, нарушение которых означает невозможность описать систему классическим образом.

Упрощенно схему квантовой телепортации можно представить себе следующим образом. Алисе и Бобу (условные персонажи) посылаются по одному фотону из пары запутанных фотонов. Алиса имеет у себя частицу (фотон) в (неизвестном ей) состоянии A; фотон из пары и фотон Алисы взаимодействуют ("запутываются"), Алиса производит измерение и определяет состояние системы из двух фотонов, оказавшейся у нее. Естественно, первоначальное состояние A фотона Алисы при этом разрушается. Однако фотон из пары запутанных фотонов, оказавшийся у Боба, переходит в состояние A! В принципе, Боб даже не знает при этом, что произошел акт телепортации, поэтому необходимо, чтобы Алиса передала ему информацию об этом обычным способом.

Как ясно из вышесказанного, возможность квантовой телепортации связана с нелокальным характером квантовой механики. В работе [1] группы ученых из Венского университета с высоким уровнем статистической достоверности экспериментально продемонстрировано, что неравенство Белла нарушается и квантовая телепортация действительно имеет нелокальную природу. В этих экспериментах квантовая телепортация осуществлялась несколько более сложным способом, чем описывалось выше; телепортируемое состояние само по себе являлось запутанным. Генерировалось две пары запутанных фотонов (на рис.1 приведена "логическая" схема эксперимента, а на рис.2 - ее приборная реализация), из каждой пары по одному фотону (0 и 3) направлялось Бобу, и по одному (1 и 2) - Алисе. Алиса производила измерение над фотонами 1 и 2, в результате чего пара фотонов оказывалась в одном из четырех возможных запутанных состояний (при этом фотоны 0 и 3 также оказывались в определенном запутанном состоянии); результаты измерения сообщались Виктору. Особенность ситуации в том, что фотоны 0 и 3 первоначально не находились в запутанном состоянии, их запутанность порождалась действиями Алисы над фотонами 1 и 2. Боб проводил поляризационные измерения над каждым из фотонов 0 и 3 (и также сообщал результаты Виктору). Виктор проводил сравнение результатов измерений и мог фиксировать нарушение неравенства Белла, что и было сделано.

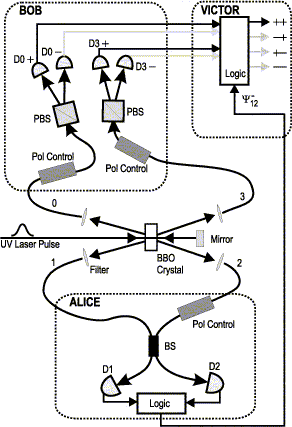
Рис.2. Схема эксперимента. Пары запутанных фотонов генерировались при прохождении импульса ультрафиолетового лазера через кристалл BaB₂O₄. После спектральной фильтрации фотоны поступали в одномодовое оптоволокно и направлялись Бобу и Алисе.

Австрийские ученые также провели эксперимент в модифицированном виде. Регистрация фотонов Бобом происходила до того как Алиса производила свое измерение. Оказалось (как и следует ожидать в рамках квантовой механики), что это никак не повлияло на результаты эксперимента. В рамках классического подхода возникает неразрешимый парадокс - позднейшее по времени действие Алисы влияет на результат более раннего действия Боба. Однако с квантовомеханической точки зрения парадокса нет: наблюдаемый эффект надо понимать так, что физическая интерпретация результатов Боба зависит от позднейшего решения Алисы.

1. Thomas Jennewein, Gregor Weihs, Jian-Wei Pan, and Anton Zeilinger. Phys.Rev.Lett. v.88, 017903 (2002).

перейти к началу страницы