Физика
Механика
Атом Бора
Следующий шаг в развитии учения о квантах сделал датский физик Нильс Бор. Он задался целью объяснить излучение отдельного атома. В твердом теле атомы в сильной степени взаимодействуют между собой и поэтому испускают непрерывный спектр излучения, который не зависит от того, из какого сорта атомов состоит твердое тело: спектры нагретых кусков меди или железа не отличаются, если температура одна и та же. Среди шума большой толпы невозможно разобрать отдельные голоса. Так и в твердом теле атомы теряют свою индивидуальность. В газах же атомы расположены далеко друг от друга и не взаимодействуют между собой, в процессе излучения, если, конечно, давление газа не слишком велико. Поэтому, когда излучает газ, «слышны голоса» отдельных атомов.
Если перед щелью спектрографа поставить колбу с водородом, светящимся под действием электрического разряда, то можно обнаружить излучение с набором волн 0,656 мкм, 0,486 мкм, 0,434 мкм и 0,410 мкм. Их принято обозначать Нальфа, Нбета, НY, Нсигма... Швейцарскому учителю И. Бальмеру удалось найти связь между этими длинами волн. Он подобрал формулу, по которой можно было бы рассчитать длины волн излучения водорода. Это было в 1885 г., а пятью годами позднее И. Ридберг придал его формуле современный вид:
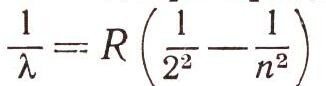
Постоянная величина R = 10967 758,1 м-1 впоследствии была названа постоянной Ридберга. Чтобы получить длину волны какой-либо линии спектра водорода, в формулу Бальмера нужно подставить вместо п одно из целых чисел: 3, 4, 5 или 6. В то время ни Бальмер, ни Ридберг и никто другой из физиков не могли объяснить, почему именно такой зависимостью связано «водородное» излучение. Бальмер верил, что в природе всюду должен царить порядок, и ему удалось просто подобрать, или, как мы говорим, получить, эмпирическую формулу. Формула оказалась точной. Разница между измеренными и вычисленными длинами волн объясняется лишь ошибками измерений.
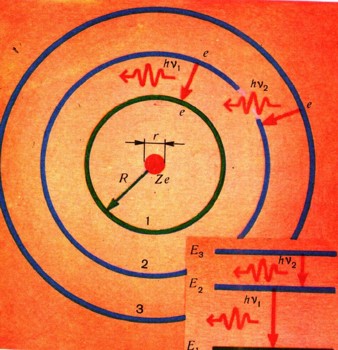
Формула Бальмера ждала своего объяснения 28 лет. В 1911 г. великий английский физик Э. Ре-зерфорд опытным путем показал, что в атоме существует положительно заряженное ядро, размеры которого малы по сравнению с размерами атома. Им же была предложена планетарная модель атома. Эта модель напоминала Солнечную систему: вокруг ядра — Солнца вращаются планеты — электроны (рис. 4). Эта аналогия еще глубже. Между ядром и электронами действуют силы притяжения, обратно пропорциональные квадрату расстояния между ними. Зависимость этих сил от расстояния такая же, как и в ньютоновском законе всемирного тяготения, управляющем движением планет.

Такие представления о строении атома хорошо согласовывались с опытными данными Резерфорда, но противоречили теории Максвелла. Из формул, выведенных Максвеллом, следовало, что «планетарный» атом не может быть устойчивым. Вращающийся вокруг ядра электрон должен все время терять энергию и в конечном итоге упасть на ядро. Но ведь атомы устойчивы! Значит, электроны в атоме не подчиняются законам Максвелла. К такому выводу пришел Ни лье Бор. В 1913 г. ему удалось найти ключ к решению проблемы устойчивости атома. Это решение опиралось на законы, определяющие оптические спектры элементов, и прежде всего спектр атома водорода.
Атом водорода — простейший. Его ядро — положительно заряженная элементарная частица — протон, вокруг которого движется отрицательно заряженный электрон. Чем ближе орбита электрона к атомному ядру, тем меньше запас энергии атома, потому что с уменьшением расстояния между двумя электрическими зарядами разных знаков их общая энергия убывает. Бор предположил, что в атоме электроны могут двигаться только по определенным орбитам, которые называют разрешенными. С орбиты на орбиту электрон переходит только скачком. Если электрон переходит с какой-то разрешенной орбиты на более близкую к ядру, то атом испускает энергию в виде кванта электромагнитного излучения (рис. 4). Если же электрон переходит на дальнюю орбиту, то для этого атом должен поглотить квант энергии, равный разности между энергией атома, когда его электрон находится на дальней орбите, и энергией атома до поглощения кванта. Иными словами, каждой из орбит электрона соответствует определенная энергия атома. Обозначим эту энергию буквой Еn, значок внизу означает номер орбиты и может принимать разные значения. Величины Еn, называют уровнями энергии атома. Бор предположил, что момент количества движения электрона по орбите носит квантовый характер и равен целому кратному п от величины
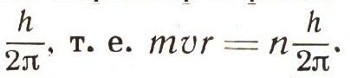
Из этого условия и условия равновесия электрона на орбите:
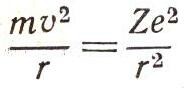
— и получается формула Ридберга. Условие равновесия электрона на орбите такое же, как и для спутника Земли или планет. В левой части
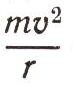
— это центростремительное ускорение электрона (т — масса электрона, v — скорость, a r — радиус орбиты), в правой части — сила, создающая это ускорение, — притяжение электрона ядром, равное по закону Кулона произведению зарядов ядра (Ze) и электрона (е), деленному на квадрат расстояния между ними. Дополнительное условие, введенное Бором, обеспечивает возможность расчета разрешенных орбит электрона, а вся эта процедура называется квантованием.
Когда атом испускает квант света с энергией hvl = E2— E1, то электрон переходит с разрешенной орбиты 2 на другую разрешенную орбиту — 1, а атом переходит с энергетического уровня Е2 на энергетический уровень Е1. По спектру свободных атомов и определяют частоты их излучений, а значит, и энергию, выделяющуюся при переходах атома с уровня на уровень, - энергетическое расстояние между уровнями.
Теория Бора - важный шаг в развитии квантовой теории излучения, квантовой механики. Эта теория объяснила процессы, происходящие в атоме при излучении. Она позволила точно "рассчитать" атом водорода. Однако объяснить с той же полнотой излучения сложных атомов она не смогла, несмотря на все попытки ее усовершенствования. Это удалось сделать после создания квантовой механики.
Атомы, содержащие большое число электронов, тоже излучают кванты света и переходят при этом с одного уровня на другой. Так, в спектре атома натрия можно видеть две близко расположенные линии желтого цвета (рис. 5). Эти линии соответствуют световому излучению с длинами волн 0,5896 мкм (эту линию называют D1) и 0,5890 мкм (линия D2).
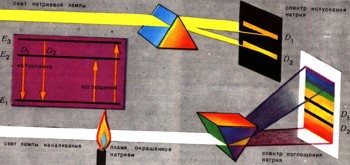
Рассчитав по формуле hv энергию-квантов, можно построить схему излучения атома натрия. Эта же схема позволяет понять, почему на месте ярких линий D1 и D2 в сплошном спектре лампы накаливания появляются темные линии, когда ее свет проходит через пламя, подкрашенное солями натрия.
Теперь расскажем о замечательной работе Эйнштейна, появившейся в 1917 г. В этой работе содержится вывод важнейшей физической закономерности - формулы Планка. В ней же впервые показано, что существует так называемое вынужденное, или индуцированное, излучение атомов - процесс, на основе которого работают лазеры, самые совершенные известные нам источники света.
Понять рассуждения Эйнштейна непросто. Поэтому читать нужно дальше с карандашом в руках. Но тот, кто решил стать физиком, не пожалеет о затраченном труде. Разве не заманчиво научиться самому выводить первую квантовую формулу, понять, что такое индуцированное излучение, и, наконец, познакомиться с настоящим квантовым расчетом, да еще сделанным самим Эйнштейном! Уже ученик 7 класса справится со всеми математическими выкладками вывода. Полезно только ближе познакомиться с показательной функцией, прочитав статью "Функция в природе и технике" в томе 2 ДЭ.
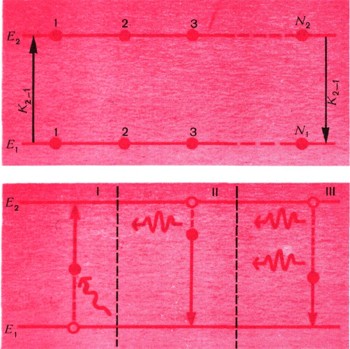
Из теории Бора следовало, что излучают отдельные атомы. В нагретом твердом теле атомы в сильной степени взаимодействуют между собой. Оказывается, это приводит к тому, что энергетических уровней, с которых атом может излучать, в нагретом твердом теле очень много. Эйнштейн рассмотрел два уровня атома с энергиями Е1 и Е2.
Атом с нижнего уровня Е перейдет на верхний Е2только в том случае, если он поглотит порцию энергии Е2-Е1, или, как теперь говорят, квант hv12 = E2-E1. Попробуем подсчитать число таких переходов, скажем, за одну секунду.
Пусть на земле под яблоней лежит N1 яблок (рис. 6). Яблоня не обычная, а квантовая. Если в плод, лежащий на земле, попадает квант hv12, то яблоко поднимается и вновь прирастает к ветке. На N\ яблок падает I(v) квантов в секунду. Вероятность того, что квант попадет в яблоко, равна S = B12I(v). В самом деле, если вы стреляете по мишени, то чем больше выстрелов сделано вами (число I(v)), тем больше шансов попадания в нее. Больше чем I(v) попаданий быть не может. Только при абсолютной меткости число попаданий могло бы равняться числу выстрелов I(v). Но квантовый обстрел ведется без всякого прицеливания, и вот величина В12 учитывает меткость этого обстрела. Конечно, она всегда меньше единицы. Теперь, чтобы получить полное число попаданий квантов в яблоки, нужно величину 5 умножить на число N1. Полное число попаданий равно числу переходов земля - ветви за секунду. Эту величину обозначим B12I(v)N1. Теперь посчитаем, сколько атомов в секунду переходит с верхнего уровня на нижний. Если на дереве N2 спелых яблок, то, естественно, чем больше N2, тем больше яблок падает на землю в единицу времени.
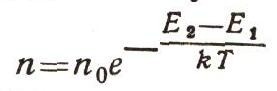
Поэтому число яблок, самопроизвольно (спонтанно, как говорят физики) падающих на землю в секунду, пропорционально числу N2. Это можно записать так:
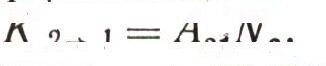
Оказывается, на квантовой яблоне число падающих на землю плодов
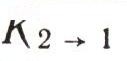
должно равняться числу
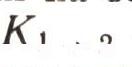
— числу вновь поднимающихся на ветви. Иначе величина I(v) менялась бы во времени, а опыт показывает, что твердое тело, находящееся в температурном равновесии, а именно такое тело мы и рассматриваем, в единицу времени испускает постоянное число квантов I(v). Приравняем теперь

и
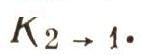
Мы получим:
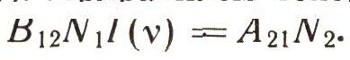
Решим это уравнение:
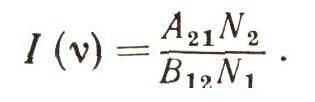
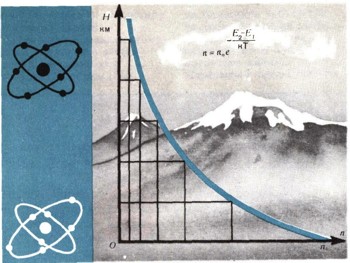
Существует замечательный закон: оказывается, если тело находится в тепловом равновесии, то число частиц с энергией E2 всегда меньше, чем число частиц с энергией Е1, когда E2 > E1 причем
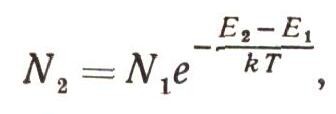
или
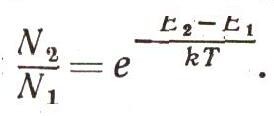
Здесь е — основание натуральных логарифмов — число, примерно равное 2,73. Величина kT — средняя кинетическая (точнее, среднеквадратичная) энергия атома тела, нагретого до температуры Т. Этот закон можно вывести строго, но доказательство слишком сложное. Между тем эту формулу стоит запомнить, она часто используется при выводе физических закономерностей (рис. 7). Теперь для зависимости силы света от частоты получим выражение
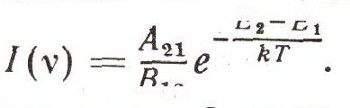
По Эйнштейну, такие кванты «вынуждают» атомы испускать себе подобные кванты. Если использовать наши «яблочные» термины, то это означает, что некоторые кванты как-то попадают в яблоки на ветвях и стряхивают их. При этом квант не поглощается, а рождается еще дополнительный квант. Число «попаданий» квантов в атомы N2 рассчитывается так же, как и число попаданий в атомы N1: оно равно B21N2. Так что на самом деле число переходов
равно A21N2 (число яблок, самопроизвольно падающих с ветвей) плюс B21N2 (число яблок, сбитых с ветвей потоком квантов с энергией hv21 и интенсивностью I(v)).
Теперь условие, вытекающее из температурного равновесия твердого тела
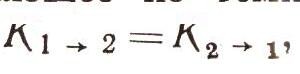
нужно записать так:
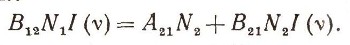
После простых выкладок вы получите
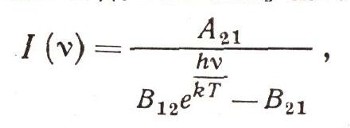
если учтете, что
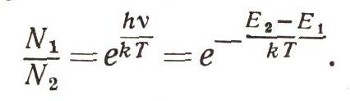
Эта формула совпадает с формулой Планка, если считать, что В12 = В21, а отношение
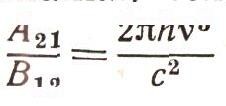
Но ведь формула Планка верна. Следовательно, и соотношения между коэффициентами A21, В12 и В21, приводящие к ней, должны быть справедливыми. Эти результаты и были получены Эйнштейном в 1917 г. Если теперь физик измерял скорость поглощения света (число переходов К1->2 за 1 с), то он уже мог вычислить и скорость вынужденного и самопроизвольного излучений, вычислить величины А21, В12и В21 — коэффициенты Эйнштейна, как мы их теперь называем. Рассчитать же теоретически сразу все три коэффициента можно только на основе квантовой электродинамики, науки, созданной через 10 лет после открытия Эйнштейна.
Вынужденное излучение в обычных источниках света играет малую роль. Поэтому если ученый, занимавшийся физической оптикой, говорил, что ему удалось из таких-то опытов определить коэффициенты Эйнштейна, то даже физики его не всегда понимали - бывали случаи, когда его коллегам, специалистам в других областях, казалось, что речь идет об опытах, связанных с проверкой теории относительности!
Потребовалось более 40 лет, чтобы открытое Эйнштейном вынужденное излучение вошло в нашу жизнь и о нем заговорили все. Ведь именно процесс вынужденного, или индуцированного, излучения -основа, на которой удалось создать мазеры и лазеры, замечательные источники электромагнитного излучения, благодаря которым совершилась революция во многих областях науки и техники.
Квантовая механика "приписывает" свойства частиц электромагнитному излучению. Но и частицы по ее законам должны проявлять в определенных условиях волновые свойства. Это, конечно, подтверждается опытом. Широко известны явления дифракции свободных электронов, нейтронов и других элементарных частиц (см. ст. "Свет"), По квантовым законам длина волны частицы с массой т, движущейся со скоростью u, равна h/mu. Так что не только электромагнитные волны обладают свойством частиц. Физик с не меньшей свободой оперирует волнами материи.
Возможно, в этой статье вы не всё поняли до конца. Да это и не удивительно, когда речь идет о проблемах, решавшихся поколениями ученых, о проблемах, приведших к созданию важнейшего раздела современной науки. Поэтому и с такими сложными понятиями сжиться по-настоящему можно, только став физиком.

Макс Карл Эрнст Людвиг Планк (1858-1947)
Немецкий физик-теоретик, член Берлинской академии наук, лауреат Нобелевской премии (1918). Наиболее важные работы Планка по термодинамической теории теплового излучения. В 1900 г. установил формулу распределения энергии в спектре излучения абсолютно черного тела (закон Планка). Пытаясь теоретически обосновать найденную формулу, Планк совершил смелый шаг, введя представления о прерывном, квантовом обмене энергией между излучающими системами. Дальнейшее развитие этой гипотезы привело к установлению теории квантов, играющей важную роль в современном естествознании. Большое значение имеют работы Планка по теории относительности и статистической физике.
2i.SU ©® 2015