Физика

Содержание раздела

Механика

Зачем нужно понятие «энтропия»

Физики совсем недавно завершили синтез алмазов. Всего несколько лет назад ученые об этом только мечтали. Столько уже было в истории науки неудачных, бесплодных попыток! Сверкающие драгоценные камни теперь не в сказке, а наяву растут в бронированной аппаратуре, под высоким давлением, при высокой температуре. На заводе синтетических алмазов могут быть теперь изготовлены самые настоящие алмазы, по своим свойствам не уступающие природным, и при этом столько, сколько их нужно технике. Разве это не подлинное чудо? Это замечательный пример того, как наука сумела осуществить сказочную мечту.

Технология синтеза алмаза трудна и сложна. Конечно, очень нелегко рассчитать и построить мощную и сложную аппаратуру. Непросто создать в ней нужное давление в десятки тысяч мегапаскалей (1 МПа = 10⁶ Па). Очень трудно при этом поддерживать высокую температуру. Но все это легко и просто по сравнению с самой главной, с самой большой трудностью, по сравнению с основной проблемой -как узнать, при каких условиях, в каких реакциях углерод может приобретать форму алмаза. Это проблема теоретического расчета, без ее решения эмпирический поиск безнадежен. Если преодолена эта трудность, все остальное разрешимо.

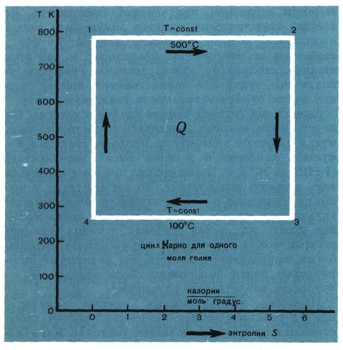
Проблема промышленного синтеза алмазов -пример типичной термодинамической задачи. Очень странные процессы использует термодинамика для своих расчетов. Квазистатический воображаемый процесс - это цепь почти равновесных состояний системы. Меняется квазистатический процесс на обратный - меняются на обратные и передачи теплоты и работы. Абсолютные их значения остаются прежними. После протекания обратимого процесса можно восстановить первоначальные состояния всех его участников - самой системы, источников тепла, источников работы - без каких-либо изменений в окружающей среде, т. е. в остальном мире. К обратимому, квазистатическому процессу предъявляются взаимно противоречивые требования: быть процессом и осуществлять равновесие, т. е. не быть процессом. Чтобы осуществить такой процесс, нужны идеальные условия, подобные тем, которые были установлены в цикле Карно.

Все реальные процессы, протекающие в действительности, нестатические - все они необратимы. Их нельзя по желанию провести в прямом и обратном направлении, не оставив никакого следа в окружающем мире. У всех изменений в природе есть определенное направление.

Термодинамика должна помочь исследователям заранее узнать, пойдет ли реальный процесс, не осуществляя его в действительности. Это и есть ее основная задача. Для этого нужно понятие "энтропия". Энтропия - это свойство системы, которое полностью определяется состоянием системы. Какими бы путями ни перешла система из одного состояния в другое, изменение ее энтропии будет всегда одно и то же. Но вычислять изменение энтропии термодинамика умеет и может только на квазистатических, обратимых путях. В этом случае изменение энтропии точно равно сумме приведенных теплот:

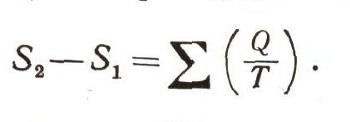
Если же в системе происходили необратимые, нестатические процессы, если в ней протекали процессы теплопередачи при конечных разностях температуры, процессы, связанные с трением, любые реальные процессы, а начальное и конечное состояния при этом были теми же самыми, то изменение энтропии будет обязательно точно таким же, но сумма приведенных теплот в необратимом процессе уже не б'удет равна изменению энтропии.

Вот поэтому-то термодинамика, рассматривает и изучает придуманные, несуществующие квазистатические процессы. Они дают возможность рассчитать и определить изменение энтропии для реальных процессов, для которых непосредственно сделать это нельзя.

Зачем ученому нужно знать энтропию

Во всех реальных процессах, при которых система может любым необратимым путем самостоятельно переходить из одного состояния в другое, общая энтропия всех участников процесса может только возрастать.

Это и дает возможность исследователю заранее предсказать, как пойдет неизвестный процесс, заранее предвидеть, при каких условиях ему удастся заставить еще не изученную на опыте реакцию пойти в нужном направлении. Для этого ученому необходимо иметь сведения об энтропии всех участников процесса, включая источники теплоты.

Химическая реакция, как и любой другой процесс, связана с работой (в результате реакции могут выделяться или поглощаться газообразные вещества или изменяться объемы реагирующих веществ и, следовательно, может совершаться работа расширения или реакция может протекать в химическом источнике тока и совершать электрическую работу и т. п.).

Химическая реакция, как и любой другой процесс, всегда сопровождается обменом тепла с окружающей средой. Если реакция идет только с поглощением тепла, систему нужно нагревать. Если тепло выделяется - охлаждать.

Для проведения расчета очень удачно то, что энтропия источников работы не может изменяться. Ведь в понятие "работа" не входят ни теплота, ни температура. Это очень сильно упрощает расчет энтропии. Изменение энтропии источников теплоты нужно обязательно учитывать, хотя это и усложняет задачу.

Если реакция, как и любой процесс, может быть проведена обратимо, то расчет изменения энтропии прост. В качестве примера можно рассмотреть любой изотермический процесс (испарение, плавление, изотермическое расширение). В этом случае существует кроме системы только один источник тепла. Их температуры одинаковы. Тепло, поглощенное системой, отдано источником (нагревателем). Насколько увеличилась энтропия системы, настолько же уменьшилась энтропия источника. Общее изменение энтропии равно нулю.

Это очень важное заключение справедливо для любых процессов, в которых участвует любое количество источников теплоты, если только эти процессы квазистатические - обратимые. Можно высказать общее положение: в любом обратимом процессе общее изменение энтропии равно нулю. Справедливо и обратное положение: если общее изменение энтропии равно нулю, то процесс обратимый. Такая зависимость очень важна. Она и позволяет ученому не наблюдать за процессом при всех условиях. Ему достаточно знать только начальное и конечное состояния системы и источников теплоты, и он сможет судить, был ли этот процесс обратимым или нет.

Обратимый процесс в сущности никуда не идет, никуда не направлен. Это цепь равновесных состояний. Реальный, необратимый, нестатический процесс такой особенностью не обладает именно потому, что он неравновесный, он самопроизвольно идет только в одну сторону. Только в том направлении может идти реальный процесс, в котором общая энтропия, т. е. энтропия системы вместе с энтропией всех источников теплоты, может только возрастать. Обратное положение тоже справедливо: если общая энтропия возрастает, то процесс необратим и может самопроизвольно протекать в нужном направлении.

Если расчет приводит к результату, согласно которому общая энтропия уменьшается, то процесс невозможен. В данном направлении он не пойдет. Всякие попытки осуществить такой процесс будут абсолютно безнадежны. Этот энтропийный принцип широко используется в науке и технике, и в первую очередь в химии и химической технологии, для суждения о том, можно ли осуществить нужную химическую реакцию или получить нужное вещество.

Для облегчения таких расчетов, часто очень сложных, существуют специальные справочные издания, в которых собраны в таблицы заранее рассчитанные значения энтропии различных химических соединений.

Как же вычислить энтропию?

Вычислить вообще энтропию системы, энтропию любого тела нельзя, точно так же, как нельзя вообще определить его энергию. Вычислить можно только изменение энтропии при переходе системы из одного состояния в другое, если этот переход провести квазистатическим путем. Расчет этот по существу прост, правда, из-за недостатка экспериментальных данных часто он становится сложным и трудным, а иногда и невозможным. Чтобы вычислить энтропию, нужны точные измерения теплоемкостей и тепловых эффектов, необходимо также знать уравнение состояния.

Чтобы получить понятие о том, как в простейшем случае рассчитывается энтропия, полезно внимательно рассмотреть график, на котором приведен расчет изменения энтропии воды.

Специального названия для единиц, в которых измеряют энтропию, не придумано. Ее измеряют

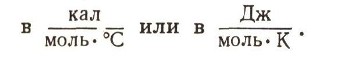
Что такое энтропия!

Много было дано ответов на вопрос, что такое энтропия, но ни один из них не может быть назван полностью удовлетворительным. Самый точный ответ такой: изменение энтропии - это сумма приведенных теплот в обратимом процессе. Ясно? Для специалиста-термодинамика ясно и достаточно. Нам же, пожалуй, стоит познакомиться еще с одним определением энтропии.

Вернемся к циклу Карно. Из всего тепла Q_H, как мы знаем, в работу можно превратить не больше чем Q_H Q_x. Тепло, отданное холодильнику, при данных температурах нагревателя и холодильника в работу уже не превратишь! Оно для нас потеряно, пропало без пользы. Сосчитать, сколько же такого обесцененного тепла, нетрудно. Не меньше чем

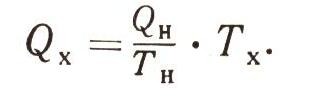
Но величина

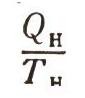
— это не что иное, как изменение энтропии нашего работающего в цикле вещества при получении им тепла от нагревания:

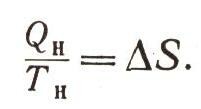
Следовательно, потерянное для нас бесполезно тепло, которое мы не можем превратить в работу, будет :

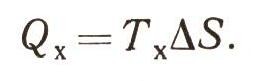
Это помогает нам дать еще одно определение энтропии, не такое строгое и точное, но чуть-чуть более наглядное: энтропия - это мера обесцененной энергии, бесполезной энергии, которую нельзя использовать для получения работы.

Так что же такое энтропия!

Как вы думаете, что произойдет, если кусок сахара положить в стакан горячего чая? Нет, это не шутка, это очень важный вопрос. Ответ на него, очевидно, всем известен. Сахар растворится, чай станет сладким. Но молекулы сахара, участвуя в тепловом движении при температуре горячего чая, могут беспорядочно двигаться в стакане куда угодно, и, в частности, любая из молекул может рано или поздно оказаться у дна стакана. В этом нет и не может быть сомнения.

Но если каждая из молекул способна на это, то почему бы им всем сразу не собраться одновременно на дне стакана, да так, чтобы снова возник бы из воды растворившийся в ней кусок сахара. Возможно это или нет? Конечно нет. Но почему?

Раскаленный конец кочерги, вынутой из печи, быстро остывает на воздухе. При этом воздух нагревается, возрастает средняя скорость его молекул. В воздухе, находящемся в термическом равновесии, существуют молекулы с разной энергией, среди них есть и очень быстрые, "горячие" молекулы. Их распределение и направление их движения беспорядочны. Каждая из таких молекул может оказаться в любом месте. Может быть, стоит подождать, пока холодная кочерга снова раскалится под ударами таких быстрых молекул? Почему бы им не собраться "случайно" всем в одном месте и не нагреть холодный металл? Возможно это? Конечно нет. Но почему?

Продырявленный футбольный мяч шипит и "испускает дух" - опадает. Но ведь молекулы воздуха движутся беспорядочно во все стороны, совершая тепловое движение. Почему бы им совершенно "случайно" не начать двигаться в одну и ту же сторону, так, чтобы дырявый мяч сам собой снова надулся? А это возможно? Ну конечно нет! Но почему?

Почему нельзя обратить явление диффузии? Почему необратимо явление теплопроводности? Почему не может само собой повыситься давление газа? И почему всегда "сами собой" идут обратные процессы выравнивания температур, выравнивания давлений, выравнивания концентраций? Все они связаны с возрастанием энтропии системы. Что это значит?

С точки зрения молекулярно-кинетических представлений все это объясняется довольно просто и наглядно: любая система стремится перейти из менее вероятного состояния в более вероятное.

Наиболее вероятное распределение молекул газа - это равномерное распределение по объему. Наиболее вероятное распределение скоростей молекул -это также совершенно определенное равномерное распределение в разных частях системы. Если в системе появятся отклонения в концентрации, температуре или давлении, то возникнут самостоятельно идущие процессы выравнивания, и они снова приведут систему в состояние равновесия - в наиболее вероятное состояние.

Чтобы лучше понять, что такое термодинамическая вероятность данного состояния газа, нужно перечитать в томе 2 ДЭ в статье "Наука о случайности" главу о вероятности. В термодинамике вероятностью данного состояния системы называют общее число способов, которыми можно это состояние осуществить, переставляя одну молекулу на место другой.

Людвиг Больцман (1844-1906)

Австрийский физик, член Венской академии наук и многих академий мира. Самыми важными работами Больцмана являются классические исследования по кинетической теории газов и статистическому истолкованию второго начала термодинамики, которые нанесли удар по идеалистической, теории тепловой смерти Вселенной. Из экспериментальных работ известны его опыты по определению диэлектрических постоянных газов и кристаллических твердых тел. В 1884 г. Больцман, используя теорию Максвелла, теоретически вывел закон Стефана (так называемый закон Стефана - Больцмана) и тем самым заложил основы современной теории излучения. Больцман проявлял большой интерес к философии, стоял на позициях стихийного материализма, активно боролся против махизма. В. И. Ленин положительно отзывался о философских взглядах Больцмана.

Связь между вероятностью данного состояния системы и ее энтропией была установлена двумя знаменитыми учеными - Д. Гиббсом и Л. Больцманом. На простом примере это можно легко показать. Известно, что энтропия любого вещества пропорциональна его массе. Это значит, что энтропия всей системы равна сумме энтропии ее отдельных частей. Разделим вещество на две части, тогда очевидно, что

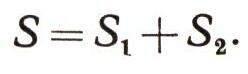
По законам теории вероятности вероятность данного состояния всей массы вещества равна произведению вероятностей его отдельных частей :

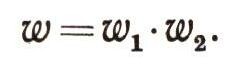
Таким образом, суммированию энтропии соответствует умножение термодинамических вероятностей состояния отдельных частей. Из всех математических функций такими свойствами обладают только логарифмы.

Таким образом, энтропия должна быть пропорциональна логарифму термодинамической вероятности:

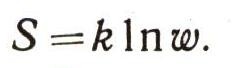
В этой формуле

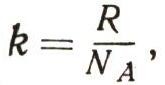
где R — газовая постоянная, N_А — число Авогадро. Следовательно, энтропия системы определяется вероятностью ее состояния. Это очень важно. Большой самостоятельный раздел науки — статистическая термодинамика, — в основе которого лежит представление о статистической природе энтропии, достиг замечательных успехов. Химикам во многих случаях теперь не нужно проводить долгие, трудные и дорогие эксперименты. Они могут рассчитывать нужные им реакции, хорошо изучив молекулярные спектры интересующих их соединений.

Стоит специально изучить эту новую, правда, трудную, но интересную и увлекательную науку даже только для того, чтобы понять, как же это оказалось возможным, изучая свет, рассчитывать и строить химические заводы.

перейти к началу страницы