Физика

Содержание раздела

Механика

Первое начало термодинамики. Закон эквивалентности тепла и работы

В 1807 г. физик Ж. Гей-Люссак, изучавший свойства газов, поставил простой опыт. Этому опыту было суждено сыграть особую роль в истории термодинамики. Случилось так, что при этом опыте присутствовали его друзья: физик и математик П. Лаплас и химик К. Бертолле. Имена этих французских ученых знают теперь все школьники мира.

Давно было известно, что сжатый газ, расширяясь, охлаждается. Правда, никто не знал почему. Гей-Люссак предположил, что это может происходить потому, что теплоемкость газа зависит от его объема. Он решил проверить это и заставил газ расширяться в пустоту - в сосуд, воздух из которого был предварительно откачан. К удивлению всех трех ученых, наблюдавших опыт, никакого понижения температуры не произошло, температура всего газа не изменилась. Исследователи не могли объяснить результат: почему один и тот же газ, одинаково сжатый, расширяясь, охлаждается, если его выпускать прямо наружу в атмосферу, и не охлаждается, если его выпускать в пустой сосуд, где давление равно нулю?

Этот опыт был неверно задуман. Полученный результат, как и следовало ожидать, не оправдал предположения ученого, и он не понял смысла опыта. Гей-Люссак и его ученые друзья сделали крупное открытие и не сумели его заметить.

Честь первой точной формулировки одного из величайших законов всего естествознания принадлежит немецкому врачу Роберту Майеру. Работая в тропиках, он заметил, что цвет венозной крови у жителей жаркого климата более яркий и алый, чем темный цвет крови у жителей холодной Европы. Наука движется странными путями, и, казалось бы, что может быть общего между расширением газа в пустоту и различием в цвете крови? Но, однако, гениальный ученый сумел найти единое в несравнимом.

Майер правильно объяснил яркость крови у жителей тропиков: вследствие высокой температуры организму приходится вырабатывать меньше теплоты, ведь в жарком климате люди не зябнут. Поэтому в жарких странах артериальная кровь меньше окисляется и остается почти такой же алой, когда переходит в вены.

У Майера возникла мысль: не изменится ли количество теплоты, выделяемой организмом, при окислении одного и того же количества пищи, если организм помимо выделения теплоты будет еще производить работу? Если количество теплоты не изменяется, то из одного и того же количества пищи можно получать то больше, то меньше тепла, так как работу организма можно снова превратить в тепло, например, путем трения. Если количество теплоты изменяется, то работа и теплота обязаны своим происхождением одному и тому же источнику - окисленной в организме пище, т. е. работа и теплота могут превращаться одна в другую.

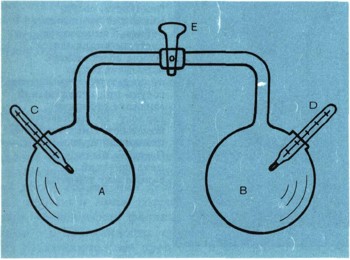
Эта замечательная идея сразу дала возможность Майеру сделать ясным загадочный результат в опыте Гей-Люссака: если теплота и работа взаимно превращаются, то при расширении газа в пустоту, когда он не производит никакой работы, так как нет никакой силы (давления), противодействующей увеличению его объема, газ и не должен охлаждаться. Если же при расширении газа ему приходится производить работу против внешнего давления, его температура должна понижаться. Даром работу получить нельзя! Но если теплота и работа могут превращаться друг в друга, если эти физические величины сходны, то возникает вопрос о соотношении между ними.

Майер первым поставил вопрос, сколько требуется работы для определенного количества теплоты и наоборот. Он очень красиво решил эту важнейшую задачу всей физики.

Давно было известно, что для нагревания газа при постоянном давлении, когда газ расширяется, нужно больше тепла, чем для нагревания газа в замкнутом сосуде, т. е. что теплоемкость газа при постоянном давлении с_р больше, чем при постоянном объеме с_v. Эти величины были уже измерены и хорошо известны. Было установлено, что, хотя обе величины с_р и c_v зависят от природы газа, разность между ними почти одинакова для всех газов

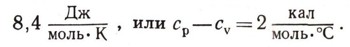
Майер понял, что эта разность в теплоте обусловлена тем, что газ, расширяясь, совершает работу. Работу одного моля расширяющегося газа при нагревании на 1° С вычислить нетрудно. Любой газ при малой плотности можно считать идеальным — его уравнение состояния было известно: pu = RT. Нагреем этот газ на 1° С, при этом он расширится, и при постоянном давлении его объем возрастет на некоторую величину дельта u. Тогда по уравнению состояния

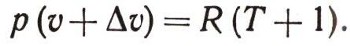
Нетрудно найти, что

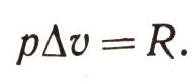
Это замечательный результат - он объясняет физический смысл газовой постоянной R. Она равна работе расширения газа при постоянном давлении, если газ нагревается на 1° С. Майер нашел, что для любого газа

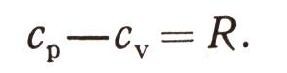
Это уравнение с тех пор носит его имя. Было известно, что величина

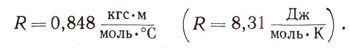
Следовательно, 2 кал равны 0,848 кгс * м работы. Нетрудно вычислить, что 1 ккал равна 424 кгс * м. Эту величину называют механическим эквивалентом тепла.

Замечательный результат Майера был много раз подтвержден прямыми измерениями; особое значение имели опыты Джоуля, который измерял количество работы, необходимое для нагревания жидкости вращающейся в ней мешалкой. Одновременно измерялись и работа, затраченная на вращение мешалки, и теплота, полученная жидкостью. Как ни менялись условия опыта, брались разные жидкости, разные сосуды и мешалки, результат был один и тот же: всегда из одного и того же количества работы получалось одно и то же количество тепла. Расчеты Майера и опыты Джоуля решили двухвековой спор о природе теплоты.

В наши дни, когда и для теплоты, и для работы применяется одна и та же мера, обе эти величины измеряются в джоулях. Доказанный Майером и Джоулем принцип эквивалентности между теплотой и работой может быть сформулирован очень просто: во всех случаях, когда из теплоты появляется работа, тратится количество тепла, равное полученной работе, и, наоборот, при затрате работы получается то же количество тепла.

Этот замечательный вывод был назван законом эквивалентности. Согласно этому закону работу можно превратить в теплоту и, наоборот, теплоту - в работу, причем обе эти величины равны друг другу.

Внимательный читатель, наверное, уже заметил, что это, конечно, справедливо только для кругового процесса, когда система совершает цикл и возвращается в исходное состояние. Расчеты Майера и опыты Джоуля касались именно таких термодинамических циклов. В каждом случае при расчете учитывалось, что система (газ, жидкость) должна быть приведена к исходным условиям.

Таким образом, для любого кругового процесса совершенная системой работа А равна полученной системой теплоте Q (если измерять и теплоту и работу в одних и тех же единицах): A = Q, или Q - A=0.

Это уравнение и выражает первый закон эквивалентности: нельзя осуществить цикл, в котором система произвела бы работу и не получила бы теплоту. В качестве примера можно взять любую тепловую машину. Все они могут работать только на основе циклов: ведь каждая из них должна работать непрерывно.

Внутренняя энергия и первое начало термодинамики

Система, совершив цикл, восстановила свое исходное состояние. В ней ничего не изменилось - ни вещество, ни движение. Для кругового процесса величина

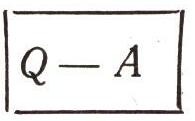
равна нулю. Из этого следует очень важный вывод, и его надо хорошо продумать и усвоить: для некругового процесса эта величина должна зависеть только от начального и конечного состояния системы, но не от пути перехода. Это очень важно. Это значит, что существует для каждой термодинамической системы величина, обладающая всеми признаками свойства системы. Это свойство и названо внутренней энергией («энергия» в переводе с греческого — деятельность). Она зависит только от состояния системы. Разность этой величины при переходе системы из одного состояния в другое равна Q — А.

Для термодинамики важно и необходимо знать разность значений внутренней энергии при переходе из одного состояния в другое. Эта величина определяется на опыте или расчетным путем по Уравнению

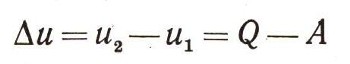
(u — обозначение внутренней энергии).

Этим замечательным уравнением выражается первое начало термодинамики. В него нужно хорошенько вдуматься. Из него вытекает, например, вся термохимия: если проводить химические реакции без изменения объема, то работа А = р*дельта y будет равна нулю. Тогда тепловой эффект реакции — теплота, поглощаемая или выделяющаяся при химических реакциях, не будет зависеть от промежуточных путей в процессе реакции. Это и есть известный закон термохимии, открытый петербургским академиком Г. И. Гессом незадолго до работ Майера.

Открытие первого начала термодинамики покончило навеки со страстной мечтой тысяч и тысяч изобретателей: создать вечный двигатель, способный работать даром, без затраты энергии. Первое начало термодинамики часто так и формулируют : вечный двигатель невозможен.

Единый закон сохранения

Физик наших дней, рассчитывая атомный реактор, конечно, тоже пользуется первым началом термодинамики, но применяет его уже в новой, обобщенной форме. Установленная А. Эйнштейном эквивалентность массы и энергии связала между собой закон сохранения вещества (важнейший закон всей химии) и закон сохранения энергии (основной закон классической физики) в единый закон сохранения - о неизменности суммы массы и энергии. Ему подчиняются все процессы и явления в микромире атомных ядер и элементарных частиц. И мы теперь знаем, что нагретое тело имеет большую массу, чем холодное.

История науки полна удивительных предвидений. М. В. Ломоносов еще в 1748 г., почти за сто лет до работы Майера, сумел впервые четко и строго высказать и сформулировать замечательную, фундаментальную мысль о единстве законов сохранения движения и материи. Он писал: "...но все изменения, совершающиеся в природе, происходят таким образом, что сколько к чему прибавилось, столько же отнимается у другого. Так, сколько к одному телу прибавилось вещества, столько же отнимется у другого... Этот закон природы является настолько всеобщим, что простирается и на правила движения: тело, возбуждающее толчком к движению другое, столько же теряет своего движения, сколько отдает от себя этого движения другому телу".

Для Ломоносова, как и для физика наших дней, великие законы сохранения вещества и сохранения энергии были единым общим законом природы.

перейти к началу страницы