Физика

Содержание раздела

Механика

Как вода течет по трубам (механика сплошных сред)

Наверное, вы думаете, что этот вопрос прост и внимания не заслуживает. Вода жидкая, она всегда и везде течет: журчит в ручейке, течет из крана, капает с крыши, струится под землей. На то она и вода. Все ясно и просто, и нет ничего особенного в том, что вода течет по трубам.

Ошибаетесь - этот вопрос далеко не так прост и очень важен. Только тот, кто хорошо разберется в том, как вода течет по трубе, поймет, почему самолет поднимается в воздух и бушуют волны на море, а мы можем петь и разговаривать.

Но те, кто еще не выучил или забыл законы Ньютона, за это пусть и не пробуют браться. Пусть лучше сначала учебник посмотрят. Итак:

Как вода течет по трубам

Задача первая

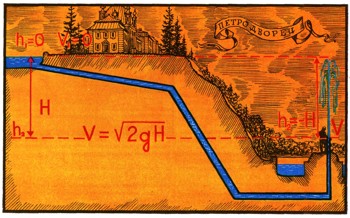
Достаточно высоко, на горе, а если хотите, то на крыше - где вам угодно, поставлена большая бочка, из нее проведена вниз труба. По трубе из бочки должна течь вода.

Что для этого надо сделать? Это задача простая. Конечно, прежде всего нужно, чтобы в бочке была вода. Из пустой бочки она не потечет. Значит, надо в бочку воду налить. Как? Ответ ясен: придется воду доставить наверх. Понятно, что надо будет хорошенько поработать - не так-то легко таскать воду в гору.

Сколько же придется затратить работы? В этом и должны помочь великий Ньютон и школьный учебник.

Решим, что в бочке помещается М килограммов воды. Много это или мало - для расчета все равно. Согласно законам Ньютона сила, с которой Земля притягивает все, что на ней находится, как и любая другая сила, равна произведению массы на ускорение. Ускорение свободного падения давно известно, оно равно увеличению скорости на g метров в секунду. Когда придется тащить воду в гору, надо будет преодолевать силу тяжести, равную Mg ньютонам. Ньютон (Н) - сила, сообщающая телу массой 1 кг ускорение 1 м/с² в направлении действия.

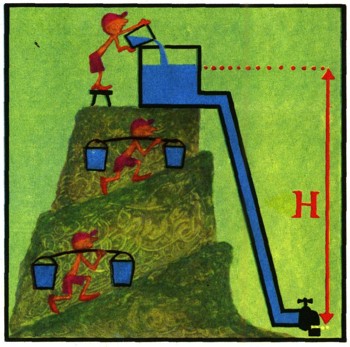
Ускорение свободного падения - величина переменная, уменьшающаяся с удалением от Земли, вблизи поверхности Земли оно равно 9,8 м/с². Работу, которую придется совершить, чтобы поднять воду на гору, вычислить нетрудно. Для этого следует умножить силу на пройденный путь. А путь в нашем случае равен высоте горы Н (заглянем еще раз в учебник). Следовательно, работа может быть вычислена по формуле

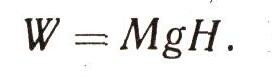
Наверное, еще многие наши читатели недолюбливают формулы. Но ничего не поделаешь! Уравнения и формулы - очень хорошие, верные помощники и друзья при решении трудных задач. Большая получилась работа или малая - решайте сами. Наверное, чтобы ее совершить, не мешает быть сильным и хорошо тренированным.

Задача вторая

Таскать воду на гору - дело тяжелое и неприятное. Удобнее качать ее снизу насосом по трубе прямо наверх, в бочку. Чему будет равна совершенная работа?

Это подсчитать нетрудно. Качать придется насосом. Чтобы подать воду наверх, придется преодолевать немалое давление столба. Единица давления равна давлению, вызываемому силой 1 Н, равномерно распределенной по поверхности площадью 1 м². Эта единица очень мала. Она называется паскаль (Па).

Пусть это давление Р Паскалей. Если площадь рабочей поверхности поршня равна S квадратным метрам, то сила, которую придется нам приложить к поршню, будет равна PS ньютонам; а если за каждое качание поршень проходит путь L метров, то работа будет равна PSL джоулей. Обратите внимание, что произведение площади поршня на длину хода SL равно объему. Следовательно, в формулу входит объем перекачанной насосом воды: Q = LS кубических метров.

Оказывается, работу насоса можно рассчитать совсем просто: она равна произведению давления на объем PQ. Качать воду вы можете сколько угодно долго и перекачать ее наверх сколько угодно много, формула от этого не изменится. Почему это так — придется сообразить самому.

Чтобы быть строгими в своем выводе, надо учесть и плотность воды (хотя она и равна почти точно единице). Обозначим ее буквой р, тогда объем воды выразится так:

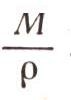
Окончательно работа, которую придется затратить, чтобы перекачать воду против давления Р, равна

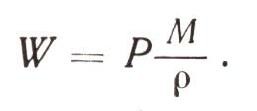
Если гора высокая и давление большое, то преодолевать его будет трудно, а если надо перекачать много воды, то качать придется долго и работу совершить немалую. Лучше это поручить мотору.

Работа совершена. Вода раньше была внизу, под горой. Теперь мы ее доставили наверх, на гору. Что изменилось?

Задача третья

Бочка полна. Можно открыть кран. Пусть вода течет вниз по трубе. Как она будет течь? Вот эта задача очень трудна. Наверное, до сих пор еще ни один самый мудрый ученый до конца не сумел ее решить. Много теоретиков ломали над ней головы. Еще больше экспериментаторов изучали в лабораториях. Тысячи томов ученых изысканий написаны и опубликованы. Но задача о том, как вода течет по трубе, так до сих пор и остается до конца еще не решенной.

Все дело в том, что вода, как и любая жидкость, обладает вязкостью. А попытка учесть вязкость в подобных задачах сразу приводит к таким сложным уравнениям, что пока еще без упрощения ни один математик в мире с ними справиться не мог.

Придется и нам задачу пока упростить. Вместо настоящей воды мы будем рассматривать воду воображаемую, такую, у которой вязкость равна нулю, т. е. совсем нет вязкости. Такая вода будет литься по трубам совсем без трения и сопротивления.

Хотя и нет жидкостей без вязкости (за исключением жидкого гелия при температуре ниже 2,19 К), но для решения нашей задачи не так уж важно -существует ли на самом деле вода, лишенная вязкости, или нет. Зато очень важно, что с таким допущением задача становится удивительно простой. Только нам придется помнить, что правильно решить упрощенную задачу еще недостаточно, надо будет подумать, каков будет прок от найденного решения. К счастью, в случае нашей задачи это допущение не очень грубое - вязкость воды невелика. Вода текуча. Это не мед, не патока и не сапожный вар.

Решать задачу теперь будет легко. Правда, решение будет не очень точным, но найти приближенный ответ тоже очень важно. Итак, мы условились, что вязкости у воды нет, поэтому можно считать, что вода по трубам течет без трения.

Но тогда совершенно все равно, где течет вода -скользит ли внутри трубы или падает вне ее, - трения ведь учитывать не надо. Просто можно считать, что она падает под действием силы тяжести, как любое тело. Задача становится совсем легкой.

Ускорение свободного падения известно, оно равно g м/с². Примем, что тело (камень, вода) падает t секунд. Скорость падения в конце пути будет равна gt м/с. Пройденный путь (а он в нашем случае равен высоте горы) будет:

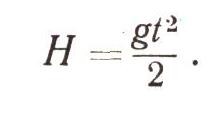
Какую же работу совершит сила тяжести, заставляя воду падать вниз? Работа всегда равна произведению силы на пройденный путь:

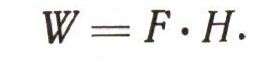
Сила тяжести равна Mg. Следовательно,

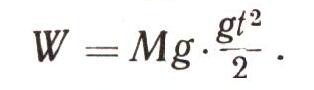
Замечательно, что существуют формулы! Они в трудный момент исследователю открывают глаза. Главное, надо научиться понимать, о чем они говорят. Полученную формулу сначала следует переписать вот так:

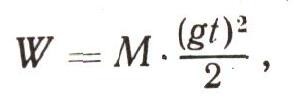
а затем, подметив, что произведение gt представляет собой скорость V, соответственно заменить в формуле. Тогда сразу станет ясно, что работа, совершенная силой тяжести, перешла в энергию движущейся воды:

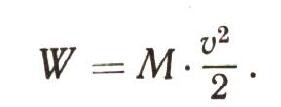
Такую работу совершает сила тяжести, пока вода стекает с горы; и, следовательно, такую же работу придется затратить для того, чтобы поднять воду обратно на гору. Это нетрудно сделать, если устроить хороший фонтан, у которого начальная скорость струи достаточно высока — не меньше, чем следует по выведенной формуле, и направлена вверх. Вспомните, как работают пожарные брандспойты.

Очень важно

Найденный нами результат очень важен. Великий закон вохранения энергии справедлив всегда. Полученная нами формула применима не только к нашему частному случаю. Работа сил, действующих на тело, не исчезает. Она переходит в его энергию движения - в кинетическую энергию, как ее называют физики.

В формулу для кинетической энергии движущегося тела входят всегда только две величины: масса и скорость. Для формулы все равно, масса ли воды или камня, мала она или велика. Любое движущееся тело: автомобиль, космический корабль, бегущий мальчишка, кулак боксера, Земля на своей орбите, электрон в атоме или в телевизионной трубке - обладает одинаково выражающейся энергией движения - кинетической энергией Mv²/2. Определить ее всегда бывает нетрудно: надо знать массу тела и измерить его скорость.

Конечно, кинетическую энергию тела, например энергию падающей воды, можно использовать для получения полезной работы самым различным образом. Вода с успехом работает на гидроэлектростанциях. Чтобы убедиться в этом, достаточно повернуть выключатель.

Формулу для кинетической энергии движущегося тела, которая нужна и ученику и академику, можно, пожалуй, с полным основанием назвать самой важной, самой главной формулой не только физики, но и всего естествознания.

Необходимое замечание

Строго говоря, в нашем рассуждении мы очень упростили задачу. Мы не обратили внимания на то, что труба может быть проложена наклонно, что на разных участках она может иметь различное сечение, и, главное, не учли, что труба будет обязательно заполнена водой полностью, без разрывов, и поэтому внутри трубы поток не может течь с ускорением. Через любое сечение трубы при установившемся потоке в каждую секунду будет протекать один и тот же объем жидкости.

Но это никак не может изменить полученного результата - закон сохранения энергии незыблем: кинетическая энергия потока будет равна работе, совершенной силой тяжести. Вопросом о том, как фактически распределится ускорение в системе, мы сейчас заниматься не будем. Впрочем, вы и сами можете подумать над этой интересной темой. Закон постоянства потока в различных сечениях трубы очень важен. Он выражается простыми уравнениями, которые называются уравнениями неразрывности:

Эти уравнения — прямое следствие закона сохранения массы вещества. Они обозначают, что через любое сечение трубы проходит одна и та же масса жидкости за одно и то же время. Так как М = vsp, а мы считаем, что жидкость несжимаема, то v₁s₁ = v₂s₂ = ... = const. Из этих уравнений следует вывод: в узком сечении трубы скорость потока большая, в широком сечении скорость его мала.

Теперь следует немного подумать...

Конечно, задачи, которые мы только что решали в порядке подготовки, не очень сложны, но все же к полученным результатам надо внимательно присмотреться и над ними подумать.

Обсуждая, как поднять воду наверх, мы сообразили, что это можно сделать по крайней мере тремя способами: просто перетаскать ее, хотя бы в ведрах, наверх; подать воду снизу насосом; воспользоваться для этой цели струей из пожарного брандспойта, хотя это и не очень удобно.

Соответственно в результате нашего исследования мы сумели найти три выражения для работы, которую нам придется для этого затратить. В первом способе приходится непосредственно поднимать воду на гору и затрачивать работу MgH. Во втором — работа производится против давления Р и равна

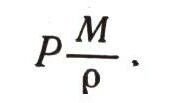
Чтобы можно было воспользоваться третьим способом, надо придать струе начальную скорость v, чтобы струя по крайней мере достигла вершины. Для этого необходима работа

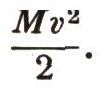
Разумеется, что если каждый раз поднимать одно и то же количество воды на одну и ту же высоту, то и затраченная работа будет тоже одна и та же, какой бы способ для подъема мы ни применяли. Это тоже следует из закона сохранения энергии.

Только не надо забывать, что при выводе мы пренебрегли такими обстоятельствами, как затрата работы на преодоление трения, при котором энергия бесполезно рассеивается, превращается в тепло. Полученные нами выражения имеют поэтому приближенный характер. Но не следует беспокоиться -

точность полученного результата нам будет вполне достаточной.

Понимать и истолковывать формулы часто бывает не так-то просто. Нужно уметь обращать внимание и учитывать значения не только тех величин, которые в них явно входят, но и тех, которые в формулах отсутствуют; а это-то как раз часто и бывает наиболее важным.

Присмотримся теперь к найденным выражениям еще раз повнимательнее: во все три формулы входит масса - заметим и запомним это; в первой нет ни давления, ни скорости; во второй нет ни скорости, ни высоты; в третьей отсутствуют высота и давление.

И это очень важно, так как отсюда следует, что если вода поднята на некоторую высоту, то все равно, будет ли она течь или находиться в покое, будет ли она сжата или нет, по выведенной формуле можно вычислить увеличение ее запаса энергии, связанное с подъемом. Если вода сжата до большого давления, то нам все равно, где она находится - вверху или внизу, течет она или нет, мы так же легко и просто рассчитаем, насколько возрастет ее энергия. А уж если вода течет, то безразлично где - внизу или наверху, под давлением или нет. Кинетическая энергия ее от этого зависеть не будет.

Только теперь мы можем приступить к решению основной задачи.

Задача главная, с удивительным решением

Бочка наполнена. Труба проложена. Откроем кран - вода потечет по трубе. Как она будет течь? Все необходимое для приближенного решения этой задачи мы уже подготовили и теперь можем без особого труда вывести закон, управляющий течением воды по трубам.

Вы, конечно, помните, что мы условились считать воду лишенной вязкости. Отметим, что мы незаметно сделали еще одно допущение: приняли, что вода несжимаема, а то нам пришлось бы учитывать работу сжатия. Но вода и на самом деле почти несжимаема.

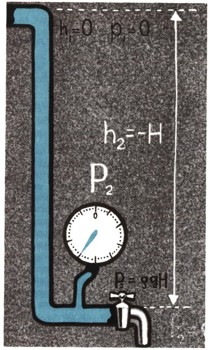
Итак, кран открыт. Вода течет по трубе. Вытекает она из емкости, поднятой на достаточно большую высоту Я, где энергия воды равна W джоулей, и мы умеем теперь ее без труда вычислять.

Чтобы найти решение нашей главной задачи, мы поступим очень просто. Представим себе, что где-нибудь, в любом месте на склоне горы, на высоте всего h метров мы выбрали произвольно какой-нибудь достаточно короткий участок трубы и установили на

нем измерительные приборы: манометр — для измерения давления и расходомер — для определения скорости потока. Ясно, что они могут быть установлены только ниже того уровня, где находится запас воды. Измерим точно давление в трубе на выбранном участке. Оно обязательно каким-нибудь да будет. Пусть оно окажется равным р паскалей. (Конечно, р<Р, этого и объяснять не требуется.) Измерим на том же участке скорость потока в трубе. Пусть она будет равна v м/с.

Вот теперь мы легко можем найти выражение для полной энергии воды, протекающей по трубе на выбранном нами коротком участке. Вода на этом участке находится на высоте всего лишь только h метров. Теперь мы можем сразу написать величину соответствующей части ее энергии. Она равна Mgh.

Вода сжата под давлением, которое мы измерили и нашли, что оно равно р паскалей. Следовательно, вода обладает еще дополнительной энергией:

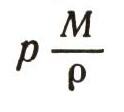
В то же время вода течет по трубе со скоростью v м/с. Ее кинетическая энергия равна

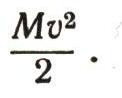
Полный запас энергии воды на высоте h, при давлении р, текущей со скоростью v, очевидно, будет равен

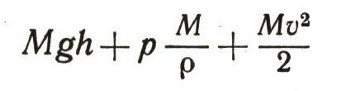
Чему же эта сумма должна быть равна? Мы условились, что трение отсутствует. Значит, некуда расходоваться тому запасу энергии, который мы сообщили воде, подняв ее наверх.

Следовательно, на основании закона сохранения энергии, сколько энергии у воды было наверху, столько же будет на любом участке движения воды по трубе:

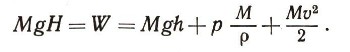
Это уравнение хотя и сложно с первого взгляда, но зато таит в себе так много интересного и неожиданного, что стоит преодолеть его сложность и не только с ним познакомиться, но и подружиться.

Прежде всего постараемся уравнение упростить. Сначала сократим массу воды, она ведь стоит и в правой и в левой части уравнения. Она от этого из уравнения не исчезнет, хотя и не будет в нем написана. Просто запомним, что мы в дальнейшем будем считать на один килограмм воды :

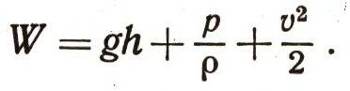
Отметим, что, как мы установили, слева в уравнении стоит постоянная величина W = const.

Теперь можем написать окончательно удивительное уравнение:

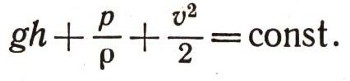
Оно может объяснить многое в том, как вода течет по трубам.

Что и как можно рассчитать с помощью выведенного уравнения!

Много интересного, полезного и важного, и к тому же очень просто. Рассмотрим сначала три самых простых, но важных случая.

1. Труба, имеющая разное сечение, проложена горизонтально. Для такой трубы высота h повсюду одинакова и, следовательно, постоянна. Поэтому уравнение станет проще:

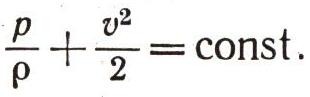
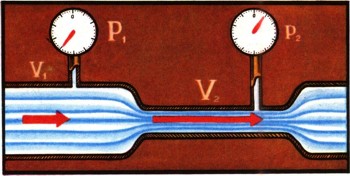
Оно по-прежнему справедливо для любого участка трубы. Из него следует удивительный и очень странный результат: там, где скорость потока будет больше (в узких участках трубы), давление обязательно должно стать меньше. А в широкой ее части давление будет большим. Что это так, убедиться нетрудно, присоединив к трубе манометры.

Картину течения воды принято изображать при помощи условных линий - линий тока. Это путь, по которому будет плыть взвешенная в потоке маленькая легкая частица. Линии тока нигде не прерываются. Там, где скорость потока выше, они сближаются теснее; там, где скорость падает, они расходятся.

2. Давление в трубе одинаково повсюду. Это допущение вполне оправдано, если труба, в которой течет вода, достаточно широкая и потерей напора на сопротивление трубы можно пренебречь (не забывайте, что вода все-таки вязкая).

Уравнение упростится по-иному:

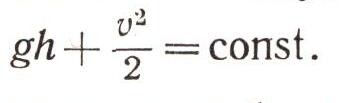
Кстати, теперь по нему удобно рассчитывать фонтаны и пожарные насосы.

3. Вода в трубе совсем не течет. Скорость равна нулю. Тогда уравнение примет новый вид:

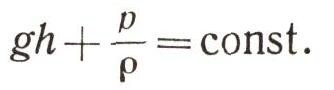
По нему теперь совсем просто рассчитывать гидростатическое давление, например, в трубах водопровода. А это необходимо, чтобы знать, насколько трубы должны быть прочны, чтобы их не разорвало.

Как видите, с помощью нашего уравнения можно многое рассчитать.

Надо теперь найденное уравнение хорошенько рассмотреть, обсудить и обдумать

Это всегда необходимо. Каждое уравнение, которое вам придется вывести самостоятельно или с которым вы познакомитесь впервые, должно быть очень внимательно рассмотрено и обсуждено. Вообще, наверное, нет ничего удивительнее математических уравнений. Они самое главное оружие человека в борьбе за овладение тайнами природы и за дружбу с ее безграничными силами. Уравнения ведут корабли в космосе; уравнения строят микроскопы, увеличивающие в миллион раз; уравнения расщепляют атом, синтезируют алмазы, строят новые заводы.

Но надо уметь понимать их. Надо уметь определять, что может дать новое уравнение, что можно от него требовать, какие оно даст возможности, когда его можно применять и когда оно неприменимо, где границы, в которых оно остается справедливым. Поэтому и нам придется обсудить записанное выше уравнение, выведенное при решении скромного, узкого и частного вопроса - как вода течет из бочки по трубе?

Рассмотрим его внимательно. Прежде всего отметим одно замечательное обстоятельство. Где в этом уравнении гора? В сущности, в нем нет на нее никаких указаний. Ее высота исчезла - сократилась. Гора оказалась не нужна. Уравнение справедливо всегда и всюду, где бы вода ни текла по трубам. Гора помогла нам вывести это уравнение, и больше она не нужна.

Тогда возникает новый вопрос: а где в выведенном уравнении трубы? В нем ведь нет ни диаметра трубы, ни ее длины. Нет ни одной величины, которая могла бы хоть как-нибудь трубу характеризовать. Значит, и трубы не ограничивают область применения полученного уравнения.

Но и это еще не все. Мы все время упорно ведем разговор только о воде. А в полученном выражении нет и намека на воду. Никакие свойства воды в нем не отражены. Вода помогала нам вывести уравнение. Но, конечно, вместо нее можно было взять любую другую маловязкую жидкость - вывод бы не изменился. Но почему только жидкость? Где в уравнении указание на то, что это именно жидкость? Из свойств вещества в него входит только плотность, которая принята постоянной, и больше ничего. Но ведь газ тоже обладает плотностью. И есть на Земле очень много процессов, в которых газ течет и не сжимается. Вспомните хотя бы ветер.

К чему же тогда применимо это замечательное уравнение? Ко всему на свете, что может течь и струиться, ко всем процессам, в которых движется маловязкая среда с постоянной плотностью. А таких процессов и таких сред в мире немало.

Ну, скажите, разве это не удивительно? Мы выводили уравнение для водопроводной трубы, а оно оказалось пригодным чуть ли не для целого света.

Это уравнение впервые вывел Даниил Бернулли

Следует помянуть добрым словом великого ученого, впервые сумевшего открыть связь между скоростью и давлением в потоке маловязкой среды и найти одно из самых важных уравнений гидродинамики. Это уравнение вывел в 1738 г. петербургский академик, замечательный математик, физик и механик Даниил Бернулли, который очень много сделал в науке.

Одним из наиболее замечательных достижений гидродинамики по справедливости до сих пор считается уравнение, с которым вы только что познакомились. Оно выражает закон сохранения энергии для текучей среды и до наших дней справедливо носит славное имя Бернулли.

Посмотрим вокруг (и прислушаемся)

Только посмотрим пристально и внимательно. Все ли для нас ясно? Всё ли мы понимаем в том, что вокруг нас происходит и что нас окружает?

Сознайтесь, что ко многому мы настолько привыкли, что даже стали воображать, что все понимаем. И давно уже перестали понимать, что на самом-то деле во многом, даже в самом простом, ровно ничего не понимаем. Нас постоянно окружает великое множество "почему?". И на многие из них, на самые простые и привычные, на самые непонятные, поможет найти ответ уравнение Бернулли.

Почему...

знамя трепещет и вьется

Ветер дует ровно. И даже если нет ветра, а просто идет колонна демонстрантов по площади и движутся они равномерно, развернутые красные знамена трепещут и колышутся. Почему же знамя не вытягивается неподвижно, не образует в ровном потоке воздуха гладкое натянутое полотнище? Почему оно трепещет и вьется как живое?

Уравнение Вернул ли легко объяснит эту загадку. Если возникнет хотя бы ничтожный изгиб, то сразу же с выпуклой стороны полотнища увеличится скорость стесненного изгибом воздушного потока; с вогнутой же стороны скорость воздуха упадет. По уравнению там, где скорость больше, давление меньше. Там, где она меньше, давление возрастет.

Разность давлений по обе стороны полотнища изогнет его еще больше, изгиб увеличится и побежит вдоль знамени как волна. Возникнет сразу новый изгиб, и знамя, подчиняясь уравнению, будет всегда трепетать как живое.

...поднимаются волны на море

Пусть над зеркальной гладью морской поверхности во время полного штиля начнет веять самый cлабый, ровный и постоянный ветерок. Если хотя бы в одном месте появится даже ничтожная неровность поверхности воды (а это всегда возможно) и возникнут еле заметные вершина и впадина волны, как тотчас же скорость ветра над гребнем волны возрастет и, согласно уравнению Бернулли, давление воздуха над волной в этом месте упадет. Над впадиной скорость воздушного потока станет меньше, а давление больше. Возникнет перепад давлений между вершиной волны и ее основанием. Этот перепад еще более поднимет гребень волны и углубит впадину между гребнями. Волнение усилится, это вызовет еще большее изменение разности скоростей ветра, что повлечет еще больший перепад давлений. Легкая волна, если ветер станет достаточно сильным, перейдет в огромные волны, опасные для мореплавателей.

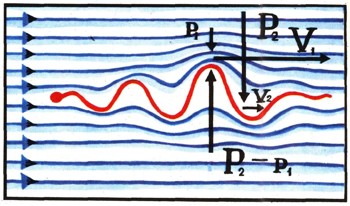
Не следует беспокоиться о том, где и как возникнет самая первая причина. Буря может начаться и там, где вильнет хвостиком рыбка.

От эффекта Бернулли зависит появление волн и их усиление, но это, конечно, не значит, что, зная одно уравнение, мы уже всё знаем о таком сложном и до сих пор еще до конца не изведанном явлении, как волны на море. Они зависят и от трения воздуха о поверхность воды, и от вязкости воды и воздуха, и от образования вихрей, и от напора ветра, и от многих других причин. Их изучает очень увлекательная и очень непростая наука, которая так и называется - физика моря.

...самолеты взлетают в небо

У каждого самолета профиль сечения крыла строго рассчитан. Верхняя поверхность крыла выпуклая. Это сделано для того, чтобы встречный воздушный поток, обтекая ее, повышал свою скорость, подобно тому как ускоряется поток воды в узком сечении трубы. Поэтому давление над крылом самолета падает очень значительно и возникает разность давлений между нижней и верхней поверхностями крыла самолета. Образующееся над крылом разрежение и поднимает самолет в небо.

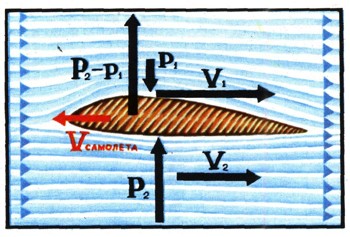
Но этим не ограничивается значение уравнения закона сохранения энергии для невязкой несжимаемой среды. Помнить и учитывать его должен конструктор, создающий новые воздушные корабли, пилот, управляющий полетом самолета.

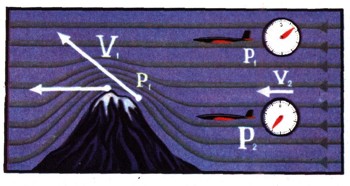
Представьте себе, что самолет должен в тумане перелететь через высокий горный хребет. В слепом полете командир ведет воздушный корабль по приборам. В его кабине обязательно находится очень важный прибор - альтиметр, который показывает высоту полета,- это точный манометр, измеряющий давление воздуха за бортом самолета. Чем выше поднимается самолет, тем ниже давление. Но если над землей бушует сильный ветер, воздушные потоки переваливают через горы и скорость ветра над вершинами может стать даже ураганной. Давление на этой высоте сильно упадет. Что будет показывать альтиметр, что может подумать летчик и что может случиться - сообразите сами.

...корабли не ходят рядом

Капитаны кораблей тоже не должны забывать о законе Бернулли. Корабли не ходят в море рядом. Почему? Разве плохо было бы после многодневного плавания в одиночестве двум кораблям, повстречавшимся в океане, пройти несколько миль рядом, бок о бок. Можно и побеседовать с новыми людьми и даже побывать друг у друга в гостях, не спуская шлюпок. Но этого делать нельзя! Почему?

Относительная скорость потока воды, сжатого между корпусами быстроходных кораблей, при их сближении сильно возрастет. Давление воды между корпусами кораблей резко упадет, и огромным напором более высокого внешнего давления корабли будут прижаты друг к другу и даже могут потерпеть аварию. Уравнение Бернулли запрещает кораблям идти в океане рядом. Моряки это знают очень хорошо.

...шипит вода, вытекая из крана

Если водопроводный кран чуть-чуть приоткрыт, то при достаточном напоре воды скорость потока в самом узком просвете крана может сильно возрасти, при этом давление понизится настолько, что даже станет ниже упругости насыщенного водяного пара, - и холодная вода в кране закипит. Образующиеся в кране мельчайшие пузырьки водяного пара, попадая в расширенную часть, где скорость потока замедляется и давление повышается, будут конденсироваться и исчезать. При этом каждый пузырек, "схлопываясь", будет издавать слабый звук. Пузырьков образуется много, их удары сливаются в непрерывный шум - вода начинает шипеть.

Точно так же вода шипит, когда начинает закипать чайник.

...мы можем петь и разговаривать

Что в гортани человека есть голосовые связки, знает каждый. Под действием струи воздуха, выходящей под давлением из легких, они колеблются. Их колебания и являются причиной возникновения звуковых колебаний воздуха. Натяжение мышечных волокон голосовых связок, изменение формы резонирующей полости гортани и полости рта определяют частоту и тембр звуковых колебаний. Поэтому-то мы и можем разговаривать и петь. Все ясно? Нет, далеко не все!

Остается неясным главное: почему воздушный поток заставляет вибрировать голосовые связки? Во время дыхания голосовые связки в гортани широко раздвинуты и воздух свободно проходит между ними с малой скоростью, поступая в легкие. В момент разговора мышечные волокна голосовых связок напрягаются, сближаются между собой и образуют узкую щель. Скорость воздушного потока резко возрастает, а давление у краев связок падает. Вследствие этого они почти смыкаются, узкая щель между ними почти полностью закрывается, скорость воздуха резко падает. Давление в просвете между краями голосовых связок возрастает вновь, и они снова расходятся, голосовая щель раскрывается. Возникает звук.

Оказывается, есть прямая связь между струей воды, вытекающей из крана, и песней жаворонка. Одно и то же уравнение многое объясняет.

Почему и как...

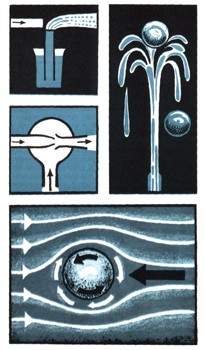
...работает обыкновенный пульверизатор;

...действуют паровые и водоструйные эжекторные насосы, применяемые на заводах для создания вакуума;

...происходит то, что вы увидите сами, если подуете вдоль бумажного листа;

...пляшет и не падает легкий шарик в струе фонтана, даже если эта струя воздушная;

...сворачивает в сторону во время полета очень быстро вращающийся - "резаный" - теннисный мяч.

И многое, многое другое, что сумеет заметить ваш внимательный глаз, попробуйте понять и объяснить самостоятельно. Постарайтесь понять, как и почему мог двигаться необычный корабль с огромными вращающимися цилиндрами вместо парусов. Сообразите, откуда должны были дуть ветры и как вращались башни-цилиндры, когда этот корабль пересекал Атлантический океан.

Можете даже сами проделать специальный опыт по демонстрации эффекта Бернулли. Опыт этот всегда удается, а результат получается очень занятный и поучительный. Надо свернуть на карандаше и склеить бумажную трубочку. Приклеить к ней на один конец диск из плотной бумаги. Это и есть демонстрационный прибор. Положите на стол бумажный лист. Поднесите диск к листу и посильнее подуйте в трубочку (рис. на стр. 96).

То, что при этом произойдет, и то, что при этом вы увидите и услышите, в объяснении уже не нуждается.

А как же все-таки течет настоящая вода по трубам (и не по трубам)!

Этот вопрос, как уже было сказано, очень труден, потому что, настоящая вода вязкая. Как происходит движение в вязкой сплошной среде, нам знать необходимо. Течет вода из крана, горючее по нефтепроводу, плывут корабли в океане, текут по равнинам реки, летят воздушные лайнеры - мы должны знать законы, управляющие их движением. Полностью все, что происходит в потоке вязкой среды, еще до сих пор не выяснено. Ученые-теоретики сумели найти самые общие уравнения, по которым, казалось бы, можно рассчитать движение жидкой среды с учетом ее вязкости, но эти уравнения оказались настолько сложными, что решить их для всех, даже практически важных, случаев и то невозможно.

Но многие интересные и важные виды потоков исследованы и изучены достаточно подробно.

Что такое вязкость

Это, наверное, удобнее всего представить себе на наглядном примере. По спокойному, очень мелкому морю, с ровным дном плывет такой большой плот, что на краевые сопротивления его бортов можно не обращать внимания.

Слой воды, прилегающий к нижней поверхности этого плота, будет смачивать ее и увлекаться плотом с той же скоростью. Слой воды у самого дна будет оставаться неподвижным. Промежуточные слои будут двигаться с разными скоростями, равномерно убывающими с глубиной. На преодоление внутреннего трения между движущимися слоями воды должна быть затрачена работа. Несмотря на то что плот движется равномерно, должна быть приложена сила F, необходимая, чтобы его тянуть. Опыт показывает, что она будет тем больше, чем больше скорость движения плота и, чем больше его площадь S и чем меньше глубина Н (рис. внизу).

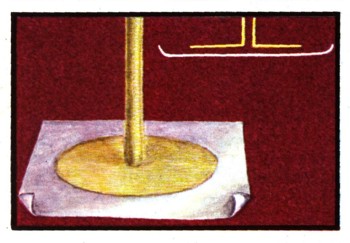
Все это можно передать простым уравнением:

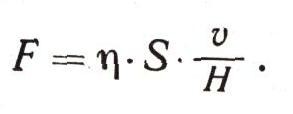
Оно выражает закон вязкого трения, также впервые установленный Ньютоном.

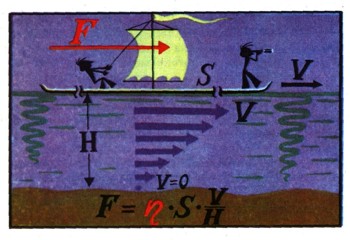
Коэффициент пропорциональности n (так называемая динамическая вязкость) определяет сопротивление движению в вязкой среде (не только в жидкой, но и в газообразной и даже в твердой — ведь из металла штампуют, вытягивают и формуют изделия).

Динамическая вязкость зависит от природы среды, она изменяется с температурой. Динамическая вязкость численно равна силе, действующей на единицу площади поверхности, находящейся в движущейся среде, в которой градиент скорости равен единице:

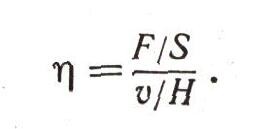
Это соотношение определяет единицу вязкости: числитель F/S имеет размерность давления и должен выражаться в паскалях, а величина H/v, обратная знаменателю, имеет размерность времени и выражается в секундах. Следовательно, размерность динамической вязкости — произведение давления и времени, а ее единица — паскаль-секунда (Па * с). Почему-то физики особого названия для этой величины придумывать не захотели.

Замечательно, что динамическая вязкость часто встречается вместе с плотностью в виде отношения

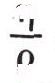
Эта величина называется кинематической вязкостью и обозначается

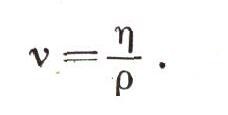
Единица кинематической- вязкости - метр в квадрате на секунду (м²/с),- несмотря на большую важность, никак не называется. Если считать, что знать, как происходит явление, - это значит уметь описать его на языке математики - уметь составить точное уравнение и уметь предсказать, как будет происходить процесс при любых условиях (т. е. уметь вычислять), то придется признаться, что, строго говоря, мы еще не знаем, как настоящая, вязкая вода течет по трубам.

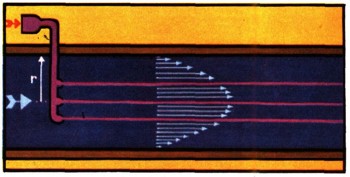
Когда не справляется теория, ей должен помочь опыт. Знакомство с движением настоящей воды по трубе проще всего начать с самого обычного примера - с обыкновенной водопроводной трубы. Если ее сделать прозрачной (хотя бы из стекла) и ввести в поток струйку раствора краски, то можно будет увидеть, что происходит в воде, текущей по трубе. А там происходит так много важного и удивительного, что стоит на этом остановиться подробнее.

По движению окрашенных струек можно наглядно изучить строение водяного потока. Рассмотрение этого очень сложного явления, конечно, удобнее начать с самого простого и доступного - с медленного потока.

Что происходит в воде, медленно текущей по трубе

Конечно, движение окрашенных струек в точности соответствует линиям тока жидкости. Они плавно следуют за всеми изменениями формы трубы, нигде не пересекаются, не искажаются, не размываются.

По скорости продвижения струйки можно легко изучить распределение скоростей в потоке внутри трубы. Оказывается, наибольшая скорость воды в центре трубы. Чем ближе к стенкам, тем она меньше; у самых стенок скорость равна нулю, жидкость словно прилипает к стенкам и остается в покое. Это совсем простой случай, его легко можно рассчитать теоретически.

Формула медленного движения воды по трубе носит имя французского физиолога Пуазейля, изучавшего движение крови в кровеносных сосудах и открывшего закон течения вязкой жидкости в трубах. Вот эта важная формула:

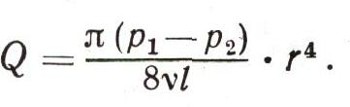
Из нее следует, что количество воды Q, протекающей по трубе за одну секунду, будет тем больше, чем выше разность давлений на концах трубы (напор); тем меньше, чем труба длиннее; тем меньше, чем больше кинематическая вязкость жидкости (например, у горячей воды вязкость меньше и ее протечет больше). Особенно сильно влияет диаметр трубы. Расход протекающей жидкости прямо пропорционален радиусу трубы в четвертой степени (r⁴). Через трубу, вдвое более толстую, воды протечет в 16 раз больше.

Уравнение Пуазейля имеет огромное значение в технике. По этому уравнению очень часто рассчитываются трубопроводы. Но следует помнить, что оно справедливо только при условии, что в трубах существует строго упорядоченный поток: такой, при котором нет перемешивания между соседними слоями текущей жидкости. Такое течение называется ламинарным. Только в ламинарном потоке введенные контрольные струйки раствора краски текут, нигде не разрываясь и не перемешиваясь.

Что происходит в быстром потоке воды

Это можно легко наблюдать на опыте с помощью тех же окрашенных струек в прозрачной трубе. Если начать постепенно повышать скорость движения воды, то сначала картина потока не изменяется. Лини,и тока остаются такими же ровными и плавными, пока скорость водяного потока не достигнет некоторого предельного значения, всегда приблизительно одного и того же для одной и той же трубы. При еще большей скорости картина внезапно и удивительным образом меняется. Плавные линии вдруг начинают колебаться, извиваться, перемешиваются, и, что особенно интересно, при тщательном изучении оказывается - в потоке возникают вихревые движения. Ламинарное, упорядоченное движение вдруг внезапно переходит в беспорядочное, обладающее очень сложной и загадочной структурой. Это турбулентное движение.

При этом меняются все свойства потока, изменяется зависимость сопротивления трубы от расхода воды, меняется профиль скоростей и вся структура потока. Но по-прежнему скорость у самых стенок трубы равна нулю.

Структура турбулентного потока, несмотря на огромное значение для современной техники, остается еще загадкой. Теория бессильна перед расчетом турбулентного потока. Практике приходится широко пользоваться опытом, выражая его результаты в виде эмпирических формул. Трудности в расчетах крыла самолета, формы космической ракеты, турбины электростанции были бы совершенно непреодолимы, если бы замечательному английскому ученому Осборну Рейнольдсу (1883) не удалось решить очень важный вопрос, который сразу сильно упростил решение многих практических задач.

Что такое "медленно" и что такое "быстро"!

Мы привыкли в обычной жизни говорить: "много" или "мало", "жарко" или "холодно", "быстро" или "медленно", не особенно задумываясь над тем, что такое "много" и что такое "мало". Где кончается "медленно" и начинается "быстро"?

Наука не терпит такой неопределенности. Наше изложение в предыдущих разделах статьи было по существу недопустимым: сказать, что при медленном движении поток ламинарный, а при быстром превращается в турбулентный, это еще почти ничего не сказать.

Что толку, если будет известно, что структура потока крови в кровеносных сосудах ламинарная, если необходимо знать, как рассчитать водоводы для гигантской электростанции. Ведь от того, какова структура потока, зависят размеры труб.

Вот на этот трудный и важный вопрос и был найден Рейнольдсом замечательный ответ. Он, проделав огромное число опытов, подметил, что если для разных труб, с различным диаметром d, и для разных жидкостей, с разной кинематической вязкостью v, так подобрать значение средней скорости потока u, чтобы величина u*d/v , характеризующая отношение инерциальных и вязких сил, оставалась постоянной, то независимо от того, каковы будут размеры труб, характер потока во всех случаях будет одинаков и вся его структура, расположение линий тока будут совершенно подобными. Отношение это еще замечательно тем, что оно безразмерно и его значение не зависит от выбора системы единиц. Обязательно проверьте это сами. Этой замечательной величине присвоено имя автора. Она называется числом Рейнолъдса и обозначается Re.

Нарисовать турбулентный поток очень трудно. Его ни один художник изобразить не сумеет. Но увидеть легко может каждый, и для этого даже не нужно окрашенных струек и прозрачной трубы. Откройте немного кран водопровода и посмотрите на вытекающую струю. Сначала она ровная, гладкая, бесшумная, прозрачная, как стеклянная палочка, -это ламинарный поток воды из крана. Теперь откройте кран полностью. Если напор достаточен, струя преобразится, помутнеет, станет неровной, начнет шипеть, ее поверхность под влиянием внутренних вихревых движений будет быстро и сильно колебаться и даже может начать разрушаться. Повышая скорость, вы перешли предельное значение числа Рейнольдса, и струя воды стала турбулентной. Это критическое, предельное значение числа Рейнольдса для течения в цилиндрических трубах равно 2000-2400.

Посмотрите на дым из трубы - это хороший пример турбулентного движения.

Водопровод, самолет, корабль турбина

Но значение числа Рейнольдса далеко не ограничивается только возможностью определения характера потока в трубе. Оказывается, совершенно сходные закономерности свойственны любому потоку вязкой сплошной среды: и тогда, когда поток протекает в трубе; и тогда, когда он обтекает на своем пути какое-либо неподвижное тело; и, конечно, тогда, когда тело движется сквозь неподвижную среду.

Если скорости малы, поток плавно обтекает встретившееся на пути тело. Линии тока огибают его, не пересекаясь и не искажаясь. Поток ламинарный. При повышении скорости характер течения вдруг меняется. На границе потока, около поверхности тела, в пограничном слое начинают возникать вихри, они уносятся потоком, сливаются вместе, образуя турбулентный след за телом. На образование этих вихрей расходуется энергия, и сопротивление тела потоку растет.

А самое замечательное в этом то, что обтекание любого тела потоком вязкой среды (воды, воздуха, любого газа, любой жидкости) определяется точно таким же числом Рейнольдса:

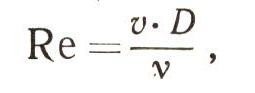
в котором u - по-прежнему скорость потока, v - кинематическая вязкость, a D в этом случае обозначает так называемый определяющий размер тела. Как бы ни отличались друг от друга по размерам два подобных тела, их взаимодействие с потоком вязкой среды будет совершенно сходно, если в соответствии с размерами будут так подобраны значения скорости и вязкости, чтобы было обеспечено равенство чисел Рейнольдса.

Не надо строить новый самолет в натуральную величину для того, чтобы изучить его поведение в полете, достаточно сделать маленькую подобную модель и испытать ее в аэродинамической трубе при таких же значениях чисел Рейнольдса.

Невозможно наугад строить гигантскую электростанцию - возможные ошибки будут стоить слишком дорого. Но можно построить точную модель всей системы: и русла реки, и плотины, и водослива, и даже самой турбины. При тех же значениях чисел Рейнольдса результаты испытаний покажут, насколько надежно и выгодно будет работать будущая электростанция.

Раньше чем заложить на верфях океанский корабль, правильность расчета его корпуса проверяют в опытовом бассейне, испытывая точную малую модель. Результаты испытаний позволяют уверенно и точно предсказать быстроходность и экономичность будущего корабля. Безгранична область применения законов механики жидкостей и газов в современной технике, бесконечны проблемы, которые решаются с ее помощью.

Казалось бы, совершенно ничем не схожи между собой турбина, корабль, плотина, самолет, нефте- и водопроводы (можно было бы привести еще множество примеров), и разве не удивительно, что наука дает возможность изучать и рассчитывать их при помощи одних и тех же законов, описывать их сходными соотношениями. Правда, уравнения современной гидродинамики часто оказываются настолько сложными, что хотя их возможно составить, но нельзя еще решить: современная математика часто бессильна перед сложностью и трудностью этих уравнений.

Но еще более удивительно, что совершенно к таким же уравнениям приводит теория явлений, связанных с взаимодействием магнитных полей и электрических токов, — электродинамика. Над этим стоит серьезно подумать.

Почему на газовых и на водопроводных трубах краны разные!

А в самом деле почему? На газовой трубе установлен простой пробковый кран. Он очень удобен. Достаточно повернуть его на четверть оборота, и линия надежно перекрыта. На водопроводных трубах стоят гораздо более сложные краны, иначе устроенные. Надо довольно долго поворачивать рукоятку крана, чтобы его внутренний клапан на винтовой нарезке постепенно перекрыл отверстие для прохода воды. Сразу такой кран никак не закроешь.

До сих пор мы рассматривали только стационарные потоки, такие, в которых скорость в каждой точке можно было считать постоянной. Гораздо сложнее будет вся картина процесса и гораздо труднее его теория, если скорость потока резко изменится.

Представьте себе, что на конце водопроводной трубы в вашем доме был бы установлен простой газовый кран. Вы налили воды в чайник и спокойно поворачиваете кран... Поток воды (плотность р) протяженностью, быть может, не одну сотню метровое большой массой М, движущийся в трубе с немалой скоростью v, обладающий большим запасом энергии, равным Mv²/2 остановился внезапно. Куда же исчезла его кинетическая энергия? Исчезнуть она не могла. Заторможенный поток может совершить за счет ее немалую работу. И он ее в этом случае обязательно совершит, да еще как!

Работа равна произведению силы на путь. Но вода почти несжимаема, трубы почти нерастяжимы. Поток остановлен внезапно. Путь, который может пройти вода в трубе после остановки за счет сжатия, ничтожно мал, близок к нулю. Следовательно, должны неминуемо возникнуть гигантские силы... и происходит неожиданная катастрофа: внезапно лопнули трубы, фонтаны воды заливают дом.

Это не выдуманная, а совершенно реальная картина. Она была обычной и причиняла много бед, пока великий русский ученый Н. Е. Жуковский, создавший теорию крыла самолета, не разработал (1898) количественную теорию, применение которой прекратило все катастрофы, вызывавшиеся таинственным гидравлическим ударом.

Теория Жуковского очень сложна, но приводит к простому результату. Чтобы вычислить величину гидравлического удара, надо знать скорость с распространения ударной волны в жидкости. При мгновенной остановке потока давление около затвора повышается на дельта р=Ро*с паскалей.

Нетрудно теперь понять, почему не нужны сложные завинчивающиеся краны на газовых линиях. Плотность газа мала, сжимаемость велика. При внезапной остановке газового потока хотя и может возникнуть повышение давления, но оно будет невелико и безопасно.

Явление гидравлического удара — это только частный пример неустановившегося движения сплошных сред. Общая теория этих процессов требует учета упругих свойств жидкости или газа. Она становится более сложной, так как приходится учитывать работу сжатия.

Вихри

Но значение замечательной области науки, с которой мы лишь вскользь познакомились, не ограничивается техникой.

Подобно тому как в вязком потоке, там, где у поверхности тела при его обтекании возникают очень высокие градиенты скоростей, появляются вдруг цепочки вихреобразных движений, очень сходные явления возникают и в природе в грандиозных масштабах. Водовороты, смерчи в пустынях и на море, торнадо, шквалы, циклоны и антициклоны в атмосфере, те чудовищные вихри на Солнце, что обычно называются просто пятнами, а может быть, даже и спиральные туманности в космосе - все эти необозримые и необъятные области явлений в мироздании, законы которых еще далеко не познаны, поразительным образом объединяются с тем, что мы наблюдаем в трубе, по которой течет вода. Все они не могут быть изучены без применения законов гидродинамики.

Возникает новая область гидродинамики, которая изучает, по каким законам энергия Солнца, падающая на нашу планету, превращается в энергию турбулентного движения - переходит от малых вихрей к более крупным и порождает в атмосфере Земли гигантские вихри - циклоны.

Физики начинают понимать, как это происходит. Создается механика глобальной общей циркуляции атмосферы с удивительным и непонятным допущением о существовании отрицательной турбулентной вязкости. Но еще никто не знает, почему это происходит. Рождение смерчей остается загадкой.

Не надо думать, что для того, чтобы познакомиться с вихревыми движениями, придется отправиться в пустыню, плавать по океанам или идти в астрономическую обсерваторию. Это можно сделать гораздо проще: помешайте суп в тарелке, вслед за движением ложки возникнут вихри; откройте спуск в вашей ванне, и вы увидите красивую картину образования воронки вихревого стока. Не следует только пытаться знакомиться с вихревыми водоворотами, купаясь у плотины.

Неньютоновские жидкости

Все, что до сих пор было рассказано в этой статье, относилось к газам или жидкостям с определенной вязкостью. Но существует огромное множество замечательных и важных жидких систем, к которым просто неприложимо понятие вязкости в том виде, в каком его установил Ньютон.

Комок сырой глины твердый, он сохраняет свою форму, а под нагрузкой глина пластична - течет. Студень на тарелке упругий и, значит, твердый, а при деформации становится жидким. А тесто твердое? Нет. Жидкое? Тоже нет. Какое оно? А знать это надо. Иначе не построишь хороших машин для хлебозаводов. Каковы свойства еще не затвердевшего бетона? А каковы свойства варенья, томатного, яблочного пюре? Каковы свойства нашей крови, растворов полимерных веществ, смазочных материалов, самых разных суспензий и эмульсий, нефти? По каким законам нефть движется под землей к буровой скважине? По каким законам она транспортируется по нефтепроводам на тысячи километров?

Все эти важные вопросы, относящиеся к веществам с аномальной вязкостью, со структурной вязкостью, к веществам, которые принято называть неньютоновскими, решаются теперь новой наукой, разделом общей механики и физики сплошных сред - реологией, наукой о пластичных свойствах вещества, о его текучести. Ведению реологии подлежат и движение крови в нашем организме, и работа смазочных масел в подшипниках быстроходных машин, и образование пластов горных пород в течение миллионов лет.

Задачи будущего

Из этой статьи вы, конечно, еще только лишь узнали, что существует большая область механики -механика сплошной среды, изучающая законы движения в сплошной вязкой среде. В этой науке много разделов: гидростатика, гидравлика, гидродинамика, аэродинамика, газодинамика, аэрогидродинамика, реология... В этой науке еще много таинственного и загадочного, в ней не решены многие, казалось бы самые простые, вопросы. Например, не решен еще до конца даже самый простой из них, сформулированный в заглавии статьи. Но в то же время эта наука помогает решать очень трудные и важные проблемы новой техники наших дней.

Уже возникают новые, огромной важности задачи, требующие дальнейшего развития механики сплошных сред. Их решение совершенно необходимо: должна быть создана теория обтекания тел такими газовыми и жидкостными потоками, в которых протекают химические реакции. Это необходимо для химии, чтобы рассчитывать и строить химические реакторы огромной мощности; необходима теория потоков, в которых совершаются фазовые превращения. Без нее нельзя строить сверхмощные экономичные паровые турбины. Конденсирующиеся из пара капли жидкой воды могут разрушить лопатки турбины и вызвать катастрофу; теория взлета космических кораблей требует развития методов расчета потоков, в которых возможна ионизация газов и возникают гигантские температурные скачки, разрушающие поверхность тела.

Очень важно уметь точно и задолго вперед предсказывать погоду, а для этого нужно знать, по каким законам происходит движение воздушных масс в атмосфере Земли и морских течений в океане. Наука встает перед загадкой существования поразительных процессов - большой области явлений с отрицательной вязкостью. Они еще далеко не изучены и не разгаданы, но, бесспорно, такие процессы играют важную роль в земной атмосфере, а знание их необходимо и для того, чтобы понять, как образуются во Вселенной спиральные галактики.

Совсем недавно родилась новая область науки -физика плазмы - среды, состоящей из заряженных частиц, из ионизированного газа (обычно при высокой температуре). Примеры плазмы: пламя, раскаленные газы, состояние вещества в звездах. Физика плазмы является теоретическим фундаментом для решения проблемы управляемого термоядерного синтеза. Путь к решению этой проблемы намечен в работах выдающегося советского физика Л. А. Арцимовича. Возникает новая отрасль химии - плазмохимия, изучающая недоступные ранее химические процессы при очень высокой температуре, превышающей десять тысяч Кельвинов.

Очень важные, очень интересные и очень нужные явления возникают при воздействии на плазму магнитных полей. Появляется принципиальная возможность прямого превращения с очень большим коэффициентом полезного действия химической энергии горения топлива в электроэнергию.

Эти гигантские задачи требуют новых методов расчета. Уже возникает новая наука - магнитогидродинамика с необъятными возможностями, но и с очень большими трудностями. Очень много работы у этой прекрасной, увлекательной, самой простой и самой сложной, самой древней и самой молодой, самой обыденной и повседневной и самой таинственной и загадочной науки - механики сплошных сред.

Вот так глина!

В природе изредка встречаются совершенно удивительные виды осадочных пород. На севере нашей страны и в Скандинавии известны особые глинистые отложения. В обычном состоянии эти твердые прочные породы ничем не отличаются от хорошо всем известных плотных глин. Но эти породы обладают поразительной способностью изменять свои свойства, когда нарушается их структура. При достаточно сильном механическом воздействии эти сухие твердые породы без малейшего добавления воды внезапно переходят в жидкое состояние. Неожиданно возникающие огромные оползни приводят к катастрофическим разрушениям и человеческим жертвам. Это странное и еще недостаточно изученное явление относится к обширной области новой науки - физико-химической механике, которая была основана замечательным советским ученым академиком П. А. Ребиндером (см. ст. "Замечательные явления на границе между телами").

перейти к началу страницы