"Спящий" волчок

Рассмотрим теперь волчок, ножка которого оканчивается не острием, как это было ранее (рис. 1), а сферической поверхностью, радиус которой невелик (рис. 16). Пусть такой волчок вращается вокруг своей оси симметрии с большой угловой скоростью омега. Отклоним ось волчка на некоторый угол от вертикали. Тогда заметим любопытное явление: волчок как бы "оживает" и без посторонней помощи ось его симметрии начинает постепенно приближаться к вертикали. Наступит момент, когда ось волчка практически совпадет с вертикалью и ее движение станет почти незаметным: волчок как бы "засыпает". Такой волчок называется "спящим". Теоретические расчеты дают возможность определить минимальную угловую скорость омега_min собственного вращения "спящего" волчка, необходимую для устойчивого его движения. Эта скорость определяется равенством

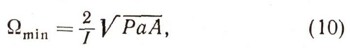
в котором все обозначения те же, что употреблялись и ранее.

Рис. 16. "Спящий" волчок.

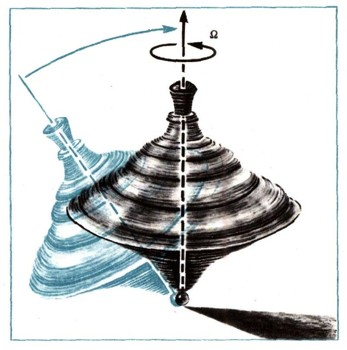
Если угловая скорость омега больше минимальной угловой скорости омега_min, то волчок будет спокойно и устойчиво вращаться вокруг вертикали; если же омега < омега_min, то он начнет раскачиваться и в конце концов упадет. Заметим, что, например, для карандаша правая часть последнего равенства соответствует примерно 30 000 об/мин. Вот почему в обычных условиях не удается вращающийся карандаш (в отличие, например, от детского волчка) заставить продолжительное время стоять на острие.

перейти к началу страницы