Почему волчок не падает?

Изложенное выше позволяет теперь объяснить движение наклонно поставленного волчка и ответить на вопрос, почему он не падает.

Рис. 14. Конец вектора собственного кинетического момента Н описывает горизонтальную окружность длиной S. Элемент дуги этой окружности совпадает с элементарным перемещением конца того же вектора при его повороте на угол w*дельта t вокруг оси воображаемой внешней рамки. Эта ось перпендикулярна вектору Н, т. е. собственной оси гироскопа, и лежит с ней в одной вертикальной плоскости.

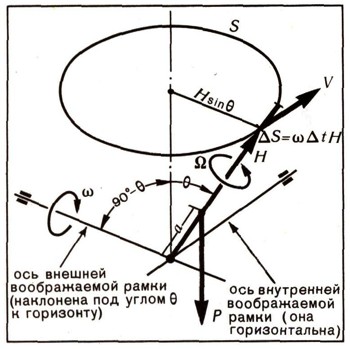
Собственный кинетический момент волчка Н выражается формулой

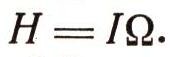
На волчок действует сила тяжести Р (рис. 14), которая в данном случае создает момент

относительно горизонтальной прямой, проходящей через точку опоры волчка перпендикулярно к его оси (заметим, что в последней формуле в — угол между вертикалью и осью волчка).

Рассмотрим движение волчка в течение малого времени дельта t. На это время оденем на волчок воображаемую внутреннюю рамку, чтобы ее ось была горизонтальной и, следовательно, совпадающей с только что упомянутой прямой (рис. 15).

Рис. 15. Воображаемые рамки, объясняющие движение волчка. Угловая скорость внешней рамки со вызывается моментом силы тяжести Р относительно прямой, проходящей через точку опоры перпендикулярно плоскости рисунка. Эта прямая одновременно является осью внутренней рамки, поворачивающейся вместе с внешней.

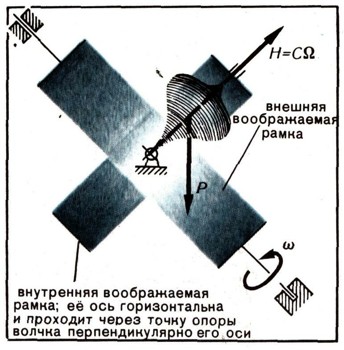
На внутреннюю рамку оденем воображаемую внешнюю, ось которой направим по перпендикуляру к горизонтальной оси внутренней рамки и собственной оси волчка. Тогда мы вернемся к только что рассмотренному случаю движения гироскопа в кардановом подвесе с той только разницей, что массу каждого кольца следует считать ничтожно малой и не учитывать при исследовании движения волчка. Гироскопические моменты и Г', описанные выше, будут теперь восприниматься только массой самого волчка.

Остановимся на случае регулярной прецессии, В течение времени дельта t воображаемая внешняя рамка вместе с волчком повернется вокруг своей наклонной оси на малый угол Да. При этом все точки оси волчка переместятся в горизонтальном направлении. Отложим на оси волчка от точки опоры отрезок, равный по длине величине собственного кинетического момента Н (рис. 14), и назовем его вектором собственного кинетического момента. Конец этого вектора переместится за время дельта t в горизонтальном направлении на расстояние

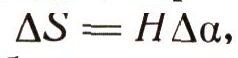
и, следовательно, его линейная скорость будет численно равна величине

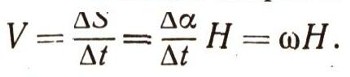
Здесь

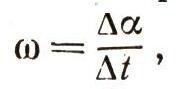
как и ранее, угловая скорость внешней рамки. Согласно полученным ранее уравнениям (3), (5) и соотношению

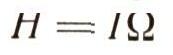
имеем для угловой скорости w следующее выражение:

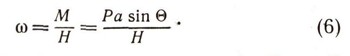
Подставим теперь это выражение в формулу V = wH для линейной скорости V конца вектора собственного кинетического момента H. Получим:

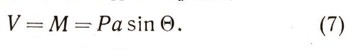
Таким образом, скорость V конца вектора собственного кинетического момента оказывается численно равной моменту М силы, приложенной к волчку относительно упомянутой выше прямой, проходящей через точку опоры. Очевидно, что при регулярной прецессии конец вектора Н будет продолжать перемещаться в горизонтальном направлении и опишет окружность длиной S = 2Пи*H*sin тета (рис. 14) вокруг вертикальной прямой, проходящей через точку опоры волчка. Если теперь разделить эту длину на скорость V = P*a*sin тета, с которой конец вектора Н движется по окружности, то придем к формуле

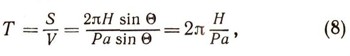
определяющей время Т обращения оси волчка вокруг вертикальной прямой. Это и есть формула для периода регулярной прецессии. Обратим внимание на то, что период прецессии не зависит от угла в отклонения волчка от вертикали, о чем уже упоминалось выше.

Как происходит псевдорегулярная прецессия волчка, уже было рассказано в начале этой статьи. Здесь укажем только, что период нутации, т. е. продолжительность повторяющихся изменений угла отклонения оси волчка от вертикали, выражается формулой

где А — момент инерции волчка относительно прямой, перпендикулярной оси собственного вращения волчка и проходящей через точку опоры (т. е. сумма произведений масс элементарных частиц волчка на квадрат их расстояния до этой прямой).

Удивительные свойства волчка используются и в цирке.

Замечательно, что от веса волчка Р и от угла в отклонения его оси от вертикали период нутации не зависит. Таким образом, один и тот же волчок на Земле и на Луне будет иметь одинаковые периоды нутации, однако в силу формулы (8) период прецессии на Луне будет больше, так как вес волчка на Луне в шесть раз меньше, чем на Земле.

перейти к началу страницы