Гироскоп под действием приложенной к нему силы

Расположим ось внешней рамки по-прежнему вертикально, а к внутренней подвесим груз Р на расстоянии а от оси внутренней рамки (рис. 13). Момент силы Р относительно этой оси при горизонтальном расположении внутренней рамки равен М = Ра.

Рис. 13. Грузик Р вызывает вращение гироскопа вокруг вертикальной оси.

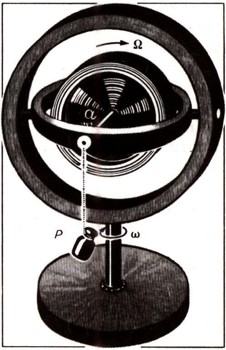
Заставим вращаться внешнюю рамку вместе с внутренней и ротором с такой угловой скоростью, чтобы соблюдалось равенство

и во время этого движения отпустим зажим на оси внутренней рамки. Как только что было указано, движение будет продолжаться так, будто бы ничего не случилось. Момент М силы Р будет все время уравновешиваться гироскопическим моментом Г, значение которого определяется формулой (2). А как будет обстоять дело, если отпустить зажим при отсутствии вращения внешней рамки или при несоблюдении равенства (3)? Тогда в это мгновение не будет равенства между моментом силы тяжести М и гироскопическим моментом Г, и, следовательно, картина последующего движения будет иной. Так, если внешняя рамка стоит на месте, то внутренняя вместе с ротором гироскопа под действием момента М силы Р вначале начнет вращаться вокруг горизонтальной оси. При таком вращении появится возрастающая угловая скорость w' вокруг этой оси, а следовательно, появится и новый гироскопический момент

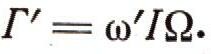
Гироскопический момент имеет вертикальное направление и, следовательно, будет стремиться повернуть весь гироскоп (т. е. его обе рамки и ротор) вокруг оси внешней рамки. Они придут в ускоренное вращение. Тем самым появится увеличивающаяся со временем их угловая скорость со вокруг вертикальной оси и соответственно возрастающий со временем гироскопический момент Г. Последний определяется по-прежнему формулой (2) и направлен против момента М силы Р. Настанет мгновение, когда оба момента, т. е. М и Г, окажутся равными. Однако после этого вращение внешней рамки вовсе не станет равномерным из-за продолжающегося движения внутренней рамки и ротора вокруг горизонтальной оси.

Гироскопический момент будет продолжать разгонять весь гироскоп вокруг вертикальной оси, и, как следствие, будет расти гироскопический момент Г. Теперь он уже станет в течение некоторого времени превышать момент М силы Р. Вращение внутренней рамки гироскопа вокруг горизонтальной оси при этом замедляется, на мгновение останавливается, и рамка начинает вращаться в обратном направлении. Гироскопический момент Г' при этом меняет знак на обратный и начинает тормозить вращение обеих рамок и ротора вокруг вертикальной оси.

Соответственно уменьшается гироскопический момент Г и наступает новое мгновение равенства его моменту М силы Р. Именно мгновение, так как из-за наличия горизонтальной составляющей угловой скорости w' внутренней рамки и ротора гироскопический момент Г' будет продолжать замедлять вращение обеих рамок и ротора вокруг вертикальной оси. В свою очередь, момент М силы Р, который теперь уже оказывается больше гироскопического момента Г, начнет замедлять вращение внутренней рамки и ротора вокруг горизонтальной оси. В результате вновь на мгновение все движение гироскопа, кроме вращения ротора вокруг собственной оси, остановится. Далее описанное движение начнет повторяться снова и снова. Перед нами картина движения, лишь в деталях отличающаяся от псевдорегулярной прецессии детского волчка, описанной в начале статьи. Можно вновь ввести апекс как точку пересечения собственной оси ротора со сферой, построенной вокруг геометрического центра волчка. Этот апекс, как следует из вышеизложенного, совершает движение между двумя горизонтальными окружностями на сфере (рис. 3). Его траектория касается нижней окружности, а на верхней окружности имеет так называемые точки возврата, т. е. подходит к ним и уходит под одним и тем же углом (прямым). Именно в этих точках апекс на мгновение останавливается.

Произведение I*омега, встретившееся в последних формулах, называется собственным кинетическим моментом ротора. Обозначается он буквой Я. Таким образом, Н = I*омега, и гироскопический момент можно определять по формуле:

перейти к началу страницы