Движение кольца в замкнутом круговом канале

Пусть теперь внутри канала движется не одна материальная точка, а целое кольцо. Заменим это кольцо совокупностью 4N отдельных связанных друг с другом материальных точек. Тогда придем к выводу, что при вращении канала вокруг основной оси, лежащей в плоскости его круговой оси кольцо будет стремиться повернуть канал вокруг поперечной оси. Момент этого воздействия представляет собой сумму моментов воздействия материальных точек, составляющих кольцо. Эту сумму нетрудно подсчитать, если каждый раз брать, например, по четыре точки, симметрично расположенные на круговой оси канала (рис. 11).

Рис. 11. Момент давления вращающегося тонкого кольца на стенки канала. Кольцо заменяется 4N равностоящими друг от друга материальными точками.

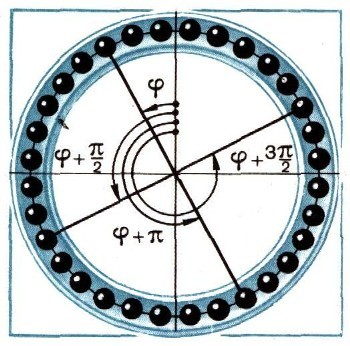
Углы, которые определяют положение таких четырех точек на этой окружности, соответственно равны величинам

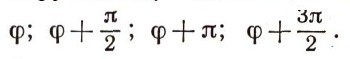
Используя простейшие формулы тригонометрии и равенство для определения момента М, получим для суммарного момента воздействия упомянутых четырех точек выражение

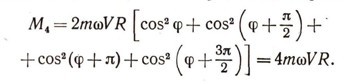
Таких четверок материальных точек будет в составе кольца ровно N, т. е.в четыре раза меньше общего числа 4N точек, составляющих кольцо. Чтобы подсчитать полный момент M₀ сил воздействия кольца на канал (по-прежнему относительно поперечной оси), следует выражение для момента М₄ умножить на N. Получим формулу М₀ = т₀w*VR, в которой m₀ = 4Nm — полная масса всего кольца.

Обозначим через омега угловую скорость кольца по отношению к стенкам канала. Тогда составляющая V скорости материальной точки относительно стенок канала определится формулой V = омега*R. Используя ее, равенство для M₀ можно представить теперь в виде

Здесь величина I = m₀R² является так называемым полярным моментом инерции кольца относительно его центра, или, что одно и то же, относительно оси, перпендикулярной к плоскости кольца и проходящей через центр его круговой оси.

перейти к началу страницы