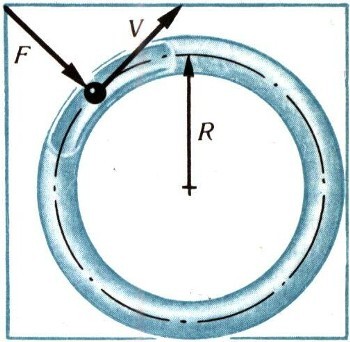
Предположим, что сила тяжести на нее не действует. Тогда единственной силой, действующей на точку, оказывается воздействие стенки канала. Вследствие абсолютной гладкости канала эта сила будет направлена перпендикулярно касательной к его круговой оси. Эту касательную следует, разумеется, проводить в том месте круговой оси, где материальная точка в данное мгновение находится. Сила воздействия стенки канала на материальную точку называется реакцией связи, так как канал связывает свободу движения точки. Если канал неподвижен, то реакция связи будет представлять собой центростремительную силу, имеющую направление к центру круговой оси канала. Она равна, как известно из курса физики, величине

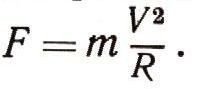
В этой формуле V — скорость точки, т — ее масса и R — радиус круговой оси канала.

Центростремительная сила направлена все время перпендикулярно скорости точки, вследствие чего не может повлиять на размер последней. Эта сила изменяет лишь направление скорости материальной точки. В самом деле, направление скорости точки непрерывно совпадает с упомянутой выше касательной и, следовательно, все время поворачивается.

Начнем теперь равномерно вращать канал вокруг неподвижной оси АА₁, расположенной в его плоскости и проходящей через центр круговой оси канала (рис. 8а).

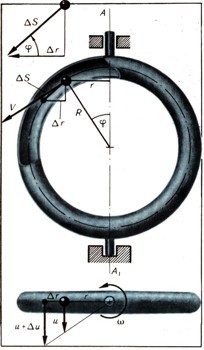
В этом случае скорость находящейся в нем точки помимо составляющей V, идущей по касательной к круговой оси канала, будет иметь составляющую и, перпендикулярную к плоскости, содержащей эту ось. Определим силу, действующую на точку в таком сложном ее движении. Рассмотрим два последовательных положения канала: в начале и в конце малого интервала времени дельта t. Канал повернется за это время на малый угол Да (рис. 86).

Отношение

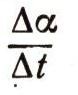
называется угловой скоростью канала. Обозначим ее через со. Таким образом,

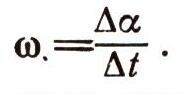
За время дельта t точка пройдет вдоль оси канала путь дельта S, причем, конечно,

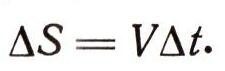
Пусть в некоторое мгновение материальная точка находится на расстоянии r от оси вращения канала. Очевидно (рис. 8а), что

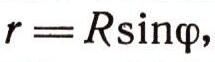
где ф — угол между осью вращения канала и радиусом R, соединяющим материальную точку с его геометрическим центром.

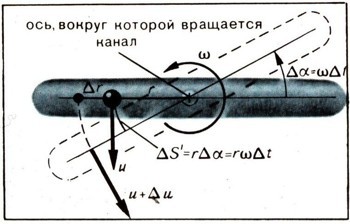
Канал вращается вокруг оси АА₁ с угловой скоростью со. Поэтому величина и составляющей скорости материальной точки в направлении, перпендикулярном к плоскости круговой оси канала, выражается формулой и = wr. Заметим, однако, что за время дельта t материальная точка успевает удалиться от оси вращения канала на расстояние дельта r. Ее боковая скорость при этом изменяется на некоторую малую величину Дм (рис. 8а). Согласно формуле и = wr имеем теперь и + дельта u = w(r + дельта r). Учитывая здесь равенство и = wr, получаем после очевидного сокращения, что дельта u = w дельта r.

При рассмотрении рисунка 8а нетрудно заметить, что имеет место приближенное равенство дельта r = дельта S cos ф, в котором дельта S по-прежнему перемещение материальной точки вдоль оси канала за время дельта t. Только что полученное равенство выполняется тем точнее, чем меньше дельта S, а следовательно, и дельта t. Поэтому, используя его в соотношении дельта u = w дельта r, получаем дельта u = w дельта S cos ф.

Разделим теперь обе части последнего равенства на дельта t и будем считать этот интервал времени исчезающие малым. В результате, учитывая, что дельта S/дельта t = V, придем к формуле w₁ = w*V*cosф, в которой введено обозначение w₁ =дельта u/дельта t. Величина w₁ представляет собой часть вектора полного ускорения материальной точки, обусловленную изменением составляющей и ее скорости в направлении, перпендикулярном к плоскости канала. Можно указать еще две части ускорения, одна из которых в точности равна w₁ и так же направлена. Происхождение этой второй части, которую обозначим через w₂, совершенно иное. Чтобы выяснить это обстоятельство, разложим, в свою очередь, составляющую скорости, направленную по касательной к каналу (т. е. вектор V), на две составляющие V₁ и V₂, направленные соответственно параллельно оси вращения канала и перпендикулярно этой оси (рис. 9).

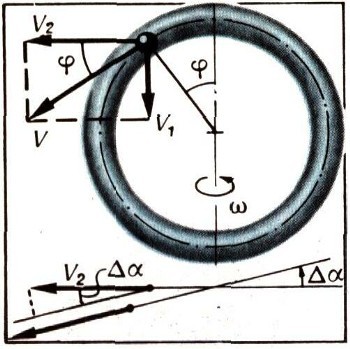
Составляющая V₂ определяется очевидной формулой V₂ = V*cosф. Спустя время дельта t эта составляющая скорости материальной точки повернется вместе с каналом на угол Да. Ее изменение в направлении, перпендикулярном к плоскости канала, мало отличается от произведения V₂дельта a. С учетом двух последних формул, а также полученного ранее соотношения дельта а = w*дельта t имеем V₂*дельта a = V₂wдельта t = V*соs ф w дельта t. Разделим это "боковое" приращение составляющей скорости V₂ на интервал времени дельта t. В результате придем к формуле W₂ = wV₂ = w Vсоs ф, в которой величина w₂ представляет собой упомянутую выше вторую часть ускорения материальной точки. Направлена она перпендикулярно плоскости канала. Обе части ускорения, т. е. w₁ и w₂, в самом деле равны и имеют одно и то же направление. Таким образом, составляющая ускорения в перпендикулярном к плоскости канала направлении выражается формулой w_р = w₁ + w₂ = 2w*V*соs ф. Третья, и последняя, составляющая ускорения, как и полное ускорение в случае неподвижного канала, направлена к центру круговой оси канала. Она равна выражению w₃ = V²/R. Заметим, что при неподвижном канале w₃ становится центростремительным ускорением точки, движущейся со скоростью V по окружности радиуса R, а составляющие w₁ и w₂ обращаются в нуль.

Если материальная точка имеет ускорение, то, согласно второму закону Ньютона, на нее непременно должна действовать сила, равная этому ускорению, умноженному на массу, и точно так же направленная, как ускорение. Поэтому в рассматриваемом случае на точку должна действовать сила со следующими двумя составляющими. Одна из них представляет собой силу, аналогичную упомянутой ранее центростремительной силе F и равную величине mw₃ = тv²/R . Другая, представляющая для нас главный интерес, выражается с учетом полученной ранее формулы для w_р соотношением Q = mw_p = 2m*w*V*соs ф. Сила Q, согласно только что изложенному, направлена перпендикулярно к плоскости канала. Она называется кориолисовой силой.

Назовем ось, вокруг которой с постоянной скоростью вращается канал, основной осью. Введем еще дополнительную ось, также расположенную в плоскости канала, но перпендикулярную основной оси, и назовем ее поперечной осью. Подвесим теперь канал на этой поперечной оси в подшипниках некоторой рамки, которая может вращаться вокруг основной оси (рис. 10).

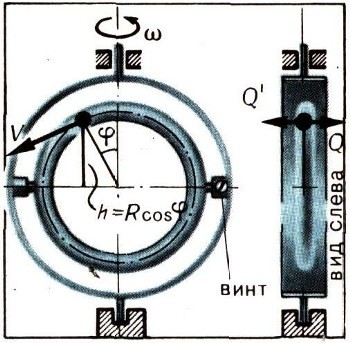
Если теперь воспрепятствовать повороту канала относительно рамки (т. е. вокруг поперечной оси), то он будет вынужден вместе с последней вращаться вокруг основной оси с угловой скоростью со. Наличие силы воздействия гладкой стенки канала на материальную точку вызывает, в соответствии с третьим законом Ньютона, равную и противоположно направленную силу, действующую уже на стенку канала. Выше были вычислены: сила Q, действующая на точку со стороны канала в направлении, перпендикулярном его плоскости, и сила F, действующая на точку в этой плоскости. Поэтому на стенку канала действуют сила Q', равная и противоположно направленная силе Q, и сила F', равная и противоположно направленная силе F. Момент силы Q относительно поперечной оси равен величине М = Q'h = Qh, где h = Rcosф — плечо силы Q' (рис. 10). Момент силы F' относительно той же оси равен нулю, так как и сила и ось лежат в одной плоскости.

Подставим теперь в выражение для момента М = Qh величину h = Rcosф, а также воспользуемся приведенным выше равенством для определения силы Q. В результате придем к формуле для момента М, а именно: М = 2mwVсоs²ф*R. Этот момент можно рассматривать как усилие, стремящееся повернуть канал вокруг поперечной оси в результате воздействия на его стенку движущейся в нем материальной точки.