Специальная теория относительности

Принципиальное значение для развития механики больших скоростей, сравнимых со скоростью 300 000 км/с, имеют исследования Альберта Эйнштейна. В своей работе "К электродинамике движущихся тел", опубликованной в 1905 г., Эйнштейн сформулировал более точную теорию механики быстродвижущихся тел - специальную теорию относительности.

В классической механике (или, как часто говорят, в дорелятивистской физике) считалось, что если мы знаем декартовы координаты х, у и время t события в некоторой неподвижной (приближенно) системе координат, то можем легко вычислить координаты х₁, у₁ и время t₁ в инерциальной системе (х₁, у₁), движущейся относительно неподвижной системы поступательно (т. е. без вращения относительно центра масс), прямолинейно и равномерно. В самом деле, если начало системы (х₁, у₁) в момент t = 0 имело координаты х₀ = 0, у₀ = 0 и система (х₁, у₁) движется вдоль оси Ох со скоростью v₀, то в момент t координаты точки х₁, у₁ будут относительно системы (х, у) следующими :

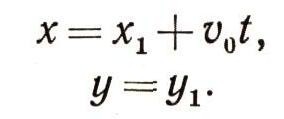
При этом чисто интуитивно предполагалось: время t в системе (х, у) течет так же, как и в системе (х₁, у₁), т. е. t= t₁; таким образом, допускалось, что течение времени не зависит от состояния движения тела. Длина масштабной линейки абсолютна, и если в покоящейся системе (х, у) некоторый отрезок имеет длину l, то он будет иметь ту же длину и в движущейся системе (х₁, у₁), иначе говоря l = l₁. В классической механике течение времени и пространственные интервалы считались независимыми друг от друга и не зависели от состояния движения системы (тела) отсчета.

В конце XIX в. накопилось достаточно большое число фактов (главным образом экспериментальных), относящихся к движению частиц со скоростями, сравнимыми со скоростью света, которые не могли быть объяснены исходя из законов классической механики.

Оказалось, что при скоростях порядка скорости света пространственные соотношения (длины отрезков) и течение времени зависят от скорости движения системы (х₁, у₁).

Исходными для построения теории относительности являются два закона природы, получившие подтверждение в самых различных явлениях движения. Эти законы были сформулированы Эйнштейном в следующем виде:

1. "Законы, по которым изменяются состояния физических систем, не зависят от того, к которой из двух координатных систем, находящихся относительно друг друга в равномерном поступательном движении, эти изменения состояния относятся".

2. "Каждый луч света движется в "покоящейся" системе координат с определенной скоростью, независимо от того, испускается этот луч света покоящимся или движущимся телом".

Первый закон распространяет закон эквивалентности инерциальных систем (закон относительности классической механики Галилея - Ньютона) на широкий класс физических явлений. Второй закон устанавливает постоянство скорости света независимо от скорости движения источника света.

Второй закон кажется наиболее парадоксальным. В самом деле, при изучении движения тел со скоростями, малыми по сравнению со скоростью света, мы убеждаемся и теоретически, и экспериментально, что скорость тела относительно неподвижной системы координат зависит от движения "платформы", с которой бросание тела производится. Так мяч, брошенный в направлении движения поезда, будет иметь по отношению к Земле большую скорость, нежели мяч, брошенный с неподвижного поезда. Для случая прямолинейного движения результирующая скорость будет равна алгебраической сумме слагаемых скоростей. При движении платформы и тела в одну сторону результирующая скорость будет равна арифметической сумме скоростей и будет подсчитываться по формуле:

где v_рез есть результирующая скорость тела по отношению к Земле, v₁— скорость платформы, v₂— скорость тела по отношению к платформе. Например, при стрельбе с летящего самолета к скорости пули по отношению к корпусу самолета нужно прибавить скорость самолета, и тогда получится скорость пули по отношению к Земле (рис. 13).

Закон сложения скоростей в теории Эйнштейна записывается иначе:

где с - скорость света.

Галилео Галилей (1564-1642).

Из уравнения (44) следует, что результирующая скорость всегда меньше скорости света. Даже в предельном случае, когда v₁ = с и v₂ = с, мы из уравнения (44) получим,что

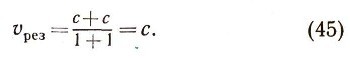
Существенные изменения претерпевают и другие основные понятия механики. Масса тела в задачах специальной теории относительности зависит от скорости движения тела:

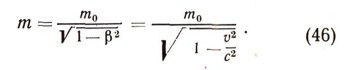
В формуле (46) т₀ — масса тела при v = 0 (масса «покоя»),т—масса тела, движущегося со скоростью V, И

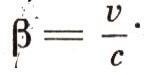
Как видно из формулы (46), масса тела неограниченно возрастает, если его скорость приближается к скорости света.

Время в теории относительности не является универсальным; для движущегося наблюдателя время течет медленнее, чем для неподвижного. Связь времен, показываемых покоящимися и движущимися часами, определяется формулой:

где to — время, отсчитываемое неподвижными часами (время в неподвижной системе координат), a t — время, показываемое часами, движущимися со скоростью v относительно неподвижной системы. Для обычных задач механики величина бета² очень мала по сравнению с единицей, и механика Ньютона дает весьма точные результаты. Так, например, если взять движение со скоростью v = 30 км/с (это примерно скорость движения Земли вокруг Солнца), то

что трудно обнаружить даже весьма точными приборами. Заметим, что при скоростях, близких к скорости света, уточнения, даваемые теорией относительности, приобретают принципиальный характер и в настоящее время, например, конструирование ускорителей, определение времени жизни элементарных частиц и экспериментальное определение массы быстродвижущихся тел не могут быть произведены без учета результатов, вытекающих из специальной теории относительности.

перейти к началу страницы