Физика

Содержание раздела

Механика

Механика тел переменной массы

Механика тел переменной массы — новая широкая область исследований в современной теоретической механике, изучающая движение и равновесие тел, масса которых изменяется во время движения. Зарождение идей об изучении движения тел переменной массы относится к концу XIX в., когда развитие ракетной техники, наблюдательной астрономии и электродинамики привело к рассмотрению нового класса задач механики, когда масса движущегося тела является или функцией времени (ракетная техника, небесная механика), или функцией скорости (специальная теория относительности). Имея в виду необычайно быстрое развитие в XX в. новых отраслей промышленности (ракетостроения и ядерной энергетики), для которых теория реактивного движения и теория относительности имеют фундаментальное значение, можно утверждать, что прогресс теоретической механики в XX столетии обусловлен в значительной степени совершенствованием методов механики тел переменной массы.

Классическая механика имеет в своей основе законы движения материальной точки, строго сформулированные Ньютоном. Почти все расчетные формулы, рекомендуемые в классической механике для характеристики движений различных объектов, имеют в качестве исходного положения второй закон Ньютона, устанавливающий простое соотношение между ускорением материальной точки, ее массой и действующими силами.

Однако второй закон Ньютона справедлив, вообще говоря, только для движений материальной точки постоянной массы. Если во время движения масса точки изменяется, то основной закон движения следует формулировать в новой, более общей форме, учитывая характеристики процесса изменения массы точки при определении ее ускорения.

В различных отраслях промышленности можно указать примеры движущихся тел, масса которых заметно изменяется во время движения. Так, масса вращающегося веретена, на которое навивается нить, увеличивается в процессе движения. Рулон газетной бумаги, который разматывается на валу печатной машины, дает нам пример тела, масса которого уменьшается с течением времени. Управляемые ракеты различных конструкций, реактивные снаряды, реактивные мины и торпеды - тела, масса которых существенно изменяется во время движения.

Случаи движения тел, масса которых изменяется с течением времени, можно видеть во многих явлениях природы. Так, например, масса Земли возрастает вследствие падения на нее метеоритов и метеорной пыли. Масса падающего метеорита, движущегося в атмосфере, убывает, так как частицы метеорита отрываются благодаря воздействию воздуха или сгорают. Масса Солнца возрастает от присоединения космической пыли и уменьшается от излучения.

Основной закон динамики точки переменной массы был открыт русским ученым профессором Петербургского политехнического института И. В. Мещерским в 1897 г. Для развития теоретической механики и особенно ее приложений в задачах динамики ракет установление исходного уравнения имеет весьма большое, принципиальное значение.

Если ограничиться рассмотрением движения точки переменной массы, то можно указать два основных фактора, влияющих на структуру уравнений движения этой точки и отличающих ее уравнения движения от уравнения Ньютона,- это переменность массы точки и принятая гипотеза отделения частиц, определяющая добавочную, или реактивную, силу. Если относительная скорость отделяющихся частиц равна нулю, то добавочная сила, обусловленная процессом отделения частиц, также равна нулю. Естественно поэтому было начать разработку теории с такого частного случая, когда реактивная сила не входит в расчеты. Результаты исследования движения .точки переменной массы при этом простом предположении были доложены Мещерским Петербургскому математическому обществу еще в 1893 г.

Последующие работы по вопросам теории движения тел переменной массы привели Мещерского к созданию строго обоснованной динамики точки переменной массы. Полученное Мещерским основное уравнение движения точки переменной массы дало возможность установить количественные закономерности для различных частных задач. Следует только подчеркнуть, что одной из существенных гипотез, лежащих в основе метода Мещерского, является гипотеза близкодействия (контактного взаимодействия тела и отбрасываемых частиц). Допускается, что в момент отделения частицы тела или точки происходит явление, аналогичное удару: частица за очень малый промежуток времени получает конечную относительную скорость и дальнейшее взаимодействие частицы и основного тела прекращается. Второй закон Ньютона получается из уравнения Мещерского как частный случай

В 1904 г. Мещерский опубликовал большую работу, посвященную изучению движения точки переменной массы с одновременным присоединением и отделением частиц. В этой работе по существу содержится теория поступательного движения реактивных аппаратов с воздушно-реактивными двигателями, хотя рассмотренные Мещерским частные задачи относились к динамике нити и движению реактивного судна.

Ценный вклад в механику тел переменной массы внес выдающийся русский ученый К. Э. Циолковский. В 1903 г. он опубликовал работу "Исследование мировых пространств реактивными приборами", в которой весьма обстоятельно исследован ряд интересных случаев прямолинейных движений тел переменной массы (ракет). Простейшая задача, решенная и исследованная Циолковским, касается возможностей самого принципа реактивного движения.

Изучая движение точки в среде без внешних сил, Циолковский показал, что при достаточно больших скорости отбрасывания частиц и отношении начальной массы точки к массе конечной можно получить весьма большие (космические) скорости. Выведенная им формула, устанавливающая связь между скоростью ракеты и ее массой, получила мировую известность и широко используется для предварительных расчетов в практике работ конструкторских бюро. Циолковский первый в научной литературе дал оценку эффективности процессов отбрасывания частиц и определил коэффициент полезного действия ракет, указав на выгодность реактивных двигателей при больших скоростях движения. В своих последующих работах (1911 -1914) он подробно изучил вопрос о запасах массы, необходимых для преодоления ракетой поля тяготения Земли, и предложил высококалорийные топлива, обеспечивающие большие скорости отбрасывания (истечения) частиц. Циолковский выдвинул много новых идей в области конструирования реактивных аппаратов для межпланетных сообщений, и его по праву считают изобретателем жидкостных реактивных двигателей, ракет дальнего действия и основоположником теории межпланетных сообщений.

В механике тел переменной массы Циолковскому принадлежит идея изучения таких движений точки переменной массы, когда в некоторых интервалах времени масса точки изменяется непрерывно, а в некоторые моменты - скачком (так называемые многоступенчатые ракеты, или поезда ракет). В задачах этого типа он первый открыл оптимальное соотношение масс ступеней поезда ракет при некоторых частных предположениях. Замечательные работы И. В. Мещерского и К. Э. Циолковского гармонично дополняют друг друга. Конкретные задачи ракетной техники, рассмотренные Циолковским, не только показали богатство практических приложений механики тел переменной массы, но и способствовали, благодаря постановке совершенно новых оригинальных проблем, развитию самой теории.

Механика тел переменной массы - наука XX в. В течение первых трех десятилетий XX в. этот раздел механики разрабатывался главным образом инженерами-ракетчиками. Было решено много интересных и важных задач о движении ракет. Опыт применения реактивного оружия во второй мировой войне явился тем реальным материалом, на основе которого строится более совершенная теория движения тел переменной массы, обеспечившая развитие ракетной техники и космонавтики. Связь теоретических изысканий в области механики тел переменной массы с актуальными задачами ракетной техники очевидна, так как масса некоторых современных одноступенчатых ракет уменьшается во время работы двигателя в 8-10 раз. В наши дни развитие этого нового раздела теоретической механики в значительной степени определяет дальнейший процесс методов классической механики.

Для механики тел переменной массы фундаментальное значение имеют два закона классической механики:

1. При любых механических процессах, протекающих в изолированной механической системе точек, без действия внешних сил, суммарное количество движения системы (вектор количества движения системы) остается постоянным.

2. Закон независимого действия сил, позволяющий складывать по правилу параллелогпамма приращение скорости точки переменной массы, обусловленное внешними силами, с приращением скорости, обусловленным действием реактивной силы, возникающей от истечения частиц из сопла реактивного двигателя.

Мещерский впервые получил основное уравнение динамики точки переменной массы для прямолинейного движения в следующем виде: та=F+Ф, (38) где т = m(t) - переменная (с течением времени) масса точки, F - равнодействующая всех внешних сил и Ф - реактивная сила. Реактивная сила пропорциональна секундному расходу истекающих из сопла двигателя частиц и их относительной (по отношению к корпусу ракеты) скорости.

Рассмотрим простейшую задачу прямолинейного движения точки переменной массы, когда F = 0. Эту задачу называют первой задачей Циолковского. В этом случае решение уравнения (38) приводит нас к формуле Циолковского, или основному закону движения ракет. Формулу Циолковского можно записать в виде:

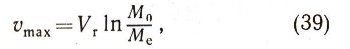
где у_mах — максимальная скорость ракеты, V_r — относительная скорость истечения частиц из сопла реактивного двигателя (скорость на срезе сопла), М₀— начальная (стартовая) масса ракеты, М_е — масса ракеты, когда все топливо израсходовано (масса ракеты без топлива). Ясно, что М₀ = М_е + т₁, где т₁ — масса топлива. Поэтому уравнение (39) можно записать в виде:

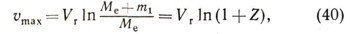
где Z = m₁/M_e — отношение массы топлива к массе ракеты без топлива, называемое числом Циолковского. В реальных конструкциях ракет число Циолковского редко превосходит значение Z = 9. Пространство, в котором F=0, называют свободным пространством. Формула выявляет максимальные возможности реактивного движения. Например, при V_r = 3000 м/с, Z = 1,0, v_max = 2079 м/с.

Из формулы Циолковского можно сделать следующие выводы:

1. Скорость точки переменной массы в конце процесса отбрасывания частиц (в конце работы двигателя) тем больше, чем больше относительная скорость отбрасывания (истечения) частиц. Если относительная скорость отбрасывания удваивается, то и скорость точки возрастает в два раза.

2. Максимальная скорость точки переменной массы возрастает при увеличении отношения начальной массы точки к ее массе в конце процесса отбрасывания частиц.

Логарифмический закон (39) был сформулирован Циолковским в 1914 г. в виде следующей теоремы: «Когда масса ракеты плюс масса взрывчатых вешеств. имеющихся в реактивном приборе, возрастает в геометрической прогрессии, скорость ракеты увеличивается в прогрессии арифметической». В самом деле, если отношение М₀/М_e будет, например, последовательно принимать значения 2, 4=2², 8=2³, 16=2⁴,..., то соответственно

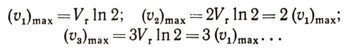
Из формулы Циолковского следует весьма важный практический вывод: для получения возможно больших максимальных скоростей ракеты (точки переменной массы) гораздо выгоднее увеличивать относительные скорости отбрасывания частиц, чем увеличивать относительный запас топлива.

Пользуясь формулой Циолковского, можно определить основные характеристики многоступенчатых ракет. Очень простой и наглядный результат получается в случае, когда приращения скорости от срабатывания последовательных ступеней одинаковы. Счет ступеней будем вести сверху вниз. Пусть М_ст есть стартовая масса первой ступени, a M₁ есть суммарная масса полезного груза и конструкции ракеты (без топлива), тогда, обозначая получим по формуле (39) скорость первой ступени:

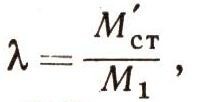
Рассмотрим теперь двухступенчатую ракету. Первая ступень для нее будет полезным грузом, а отношение

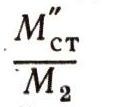
равным Лямбда. Тогда скорость, сообщаемая первой ступени (от второй), будет снова равна v₁. Но двухступенчатая ракета сообщит полезному грузу первой ступени скорость v₂ = 2v₁, или

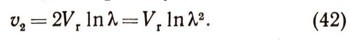
Рассуждая аналогичным образом, найдем, что трехступенчатая ракета сообщит полезному грузу первой ступени скорость

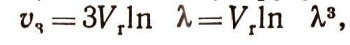
а n-ступенчатая - скорость v_n=V_r ln Лⁿ. Мы видим, что если массы последовательных ракет растут в геометрической прогрессии, то скорости полезного груза первой ступени увеличиваются в прогрессии арифметической. Найдем стартовую (начальную) массу двухступенчатой ракеты при Л=е²=7,4 (число Циолковского Z=6,4; е - основание натуральных логарифмов), если масса полезного груза первой ступени и ее конструкции равна М₁ = 10 т. Из приведенных формул следует, что первая и вторая ступени будут иметь массу :

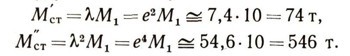
Если скорость истечения газов из сопла двигателя будет 3000 м/с, то полезный груз получит в свободном пространстве (F = 0) скорость, равную 12 км/с, т. е. немного большую второй космической.

перейти к началу страницы