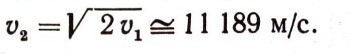Физика
Механика
Движение в поле тяготения
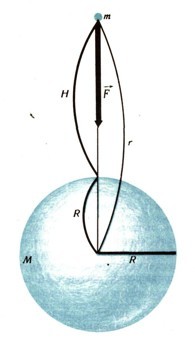
Исследования поля тяготения Земли показали, что в ряде случаев можно считать силу притяжения, обусловленную массой Земли, центральной (направленной к центру Земли) и подчиняющейся закону тяготения Ньютона, т. е.

где т - масса притягиваемой материальной точки (или сравнительно небольшого материального тела: самолета, ракеты, космического корабля и т. п.), М — масса Земли, n — постоянная тяготения (n=6,67*10-11Н*м2/кг2), r — расстояние точки от центра Земли (рис. 12).
Если считать плотность Земли функцией только расстояния от центра, то можно совершенно строго доказать, что в этом случае Земля притягивает внешнюю материальную точку, как точка, расположенная в центре Земли и имеющая массу, равную массе Земли.
Мы будем считать Землю (приближенно) сферой радиуса r = R, и на поверхности Земли силу притяжения можно записать на основании соотношения (28) как
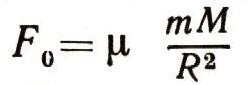
и на основании второго закона Ньютона F0 = силе тяжести = mg0, где g0 — ускорение, сообщаемое массой Земли точке, расположенной на ее поверхности. Таким образом,
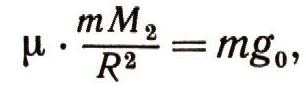
и, следовательно, гравитационную силу, обусловленную притяжением частиц земного шара для точки массой т, можно записать в виде:
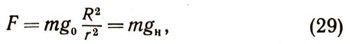
где gH - ускорение, обусловленное гравитационной силой Земли на высоте Я над поверхностью Земли
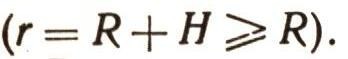
Рассмотрим движение искусственного спутника Земли по окружности радиуса R при H —> 0, пренебрегая сопротивлением атмосферы. На основании формулы (25) центростремительное ускорение спутника будет
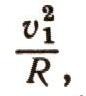
где v1—первая космическая скорость. Но, с другой стороны, это ускорение совпадает с гравитационным ускорением g0, обусловленным массой Земли. Таким образом,
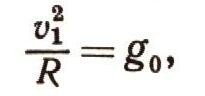
откуда первая космическая скорость
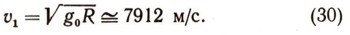
Зная v1 и длину окружности радиуса R (длину экватора, например), можно найти время полного оборота спутника вокруг Земли. Это время будет равно 84 мин 26 с. Можно по формулам (25) и (29) найти скорость искусственного спутника Земли на любой высоте Н. В самом деле, приравнивая центростремительное ускорение
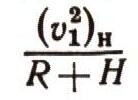
к гравитационному на высоте Н, получим:
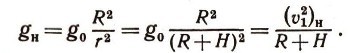
Таким образом,
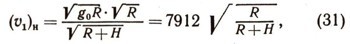
где (v1)H, - скорость спутника на высоте Н.
Первая космическая скорость убывает по закону (31) с увеличением высоты над поверхностью Земли (см. таблицу).
Таблица
| Высота спутника над поверхностью Земли — Н (в км) | Скорость спутника
(v1)H(в м/с) |
Период обращения спутника | ||
| ч | мин | с | ||
| 0 | 7912 | 1 | 24 | 26 |
| 200 | 7791 | 1 | 28 | 26 |
| 400 | 7675 | 1 | 32 | 30 |
| 1000 | 7356 | 1 | 45 | 02 |
| 3000 | 6525 | 2 | 30 | 31 |
| 6000 | 5679 | 3 | 48 | 18 |
В таблице даны значения скоростей искусственных спутников Земли, обращающихся на разных высотах по круговым орбитам, и периоды их обращения. Первая строка этой таблицы имеет чисто теоретическое значение, так как при скорости полета v = vl пренебрегать у поверхности Земли силой сопротивления воздуха нельзя.
Формула для периода обращения спутника TH будет:

Исходя из формулы (32) можно найти высоту полета Я такого искусственного спутника Земли, у которого время обращения будет равно 24 ч. (Такой спутник будет на экваторе «висеть» над вполне определенным меридианом и не двигаться относительно поверхности Земли. Мы называем теперь такие спутники геостационарными.) Простые вычисления дают H = 35810 км.
Решим теперь задачу о максимальной высоте подъема материальной точки, брошенной вертикально вверх с начальной скоростью v0. Гравитационное поле будем вначале (малые высоты подъема) считать однородным. В этом случае движение будет рав-нозамедленным и определяться по формуле
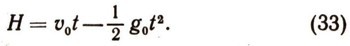
Когда точка достигает высоты Н=Нтах, то ее скорость будет равна нулю. Таким образом, имеем соотношение
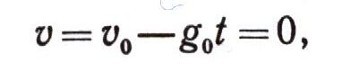
откуда

Формула (34) дает время полета до максимальной высоты Нтах. Подставляя уравнение (34) в уравнение (33), получим максимальную высоту подъема:

Эта формула впервые была получена Г. Галилеем.
Можно решить задачу о максимальной высоте подъема и в ньютоновом поле тяготения Земли, когда гравитационная сила определяется формулой (29). Это решение требует знания высшей математики. Окончательная формула для переменного поля тяготения имеет вид:
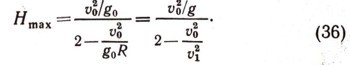
Когда скорость v0 мала по сравнению с первой космической
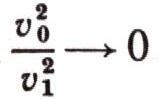
тогда из формулы (36) получается формула Галилея. Из формулы (36) можно получить величину второй космической скорости. Чтобы ракета покинула поле тяготения Земли, нужно неограниченно увеличивать Hmaх; это будет возможно, если знаменатель дроби устремить к нулю:
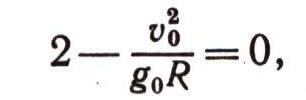
откуда

Сравнивая v1 (формула 30) с v2, находим, что