Физика
Механика
Движение по окружности
Скорость материальной точки есть векторная величина. Приращение скорости дельта v за малый промежуток времени дельта t в общем случае криволинейного неравномерного движения обусловлено изменением вектора скорости и по величине и по направлению. Рассмотрим равномерное движение материальной точки массой m по окружности радиуса r.
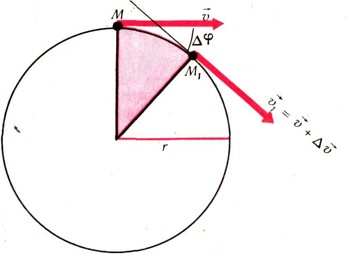
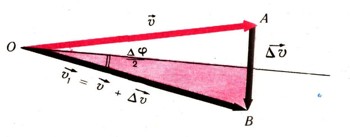
В этом случае приращение дельта v вектора обусловлено изменением только его направления. Возьмем два близких по времени (t и t + дельта t) положения движущейся точки (М и M1), тогда очевидно, что вектор v1=v+дельта v (рис. 10 и 11). Из равнобедренного треугольника ОАВ получим:
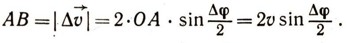
Если угол дельта ф мал, то
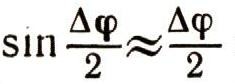
и, следовательно,
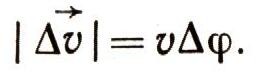
Ускорение точки М направлено к центру круга и по величине равно:
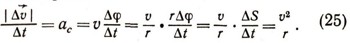
Формулу (25) можно записать в иной форме, если ввести понятие угловой скорости. Мы будем называть угловой скоростью радиуса, следящего за движущейся точкой, отношение приращения угла поворота радиуса Дф к приращению времени дельта t, т. е.

где со - угловая скорость радиуса, следящего за точкой М, движущейся по окружности. Если правую и левую части уравнения (26) умножить на r, то
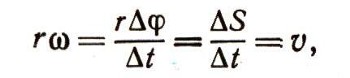
и, следовательно, центростремительное ускорение (25) можно записать в виде:
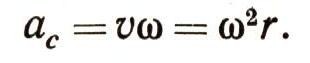
Угловая скорость со характеризует быстроту вращения радиуса, следящего за движущейся точкой М. В паспорте различных двигателей обычно указывают число оборотов в минуту. Легко выразить угловую скорость со через число оборотов п1 в минуту. В самом деле, за один оборот радиус, следящий за движущейся точкой, поворачивается на угол 2Пи; за п1 оборотов в минуту он повернется на угол 2Пи*п1,и, следовательно,
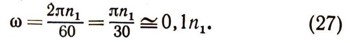
2i.SU ©® 2015