Физика
Механика
Колебания
Весьма важный случай движения представляют гармонические колебания. В большинстве случаев гармонические колебания возникают при действии упругой силы, подчиняющейся закону Гука. Рассмотрим в качестве простейшего примера колебания груза, подвешенного на пружине (рис. 8).
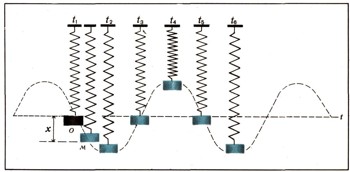
Начало координат возьмем в положении равновесия груза. Если отклонить груз на расстояние ОМ = х, то возникнет сила F = kx, которая будет стремиться возвратить груз в точку О; часто эту силу называют восстанавливающей, а коэффициент k — коэффициентом жесткости пружины. Согласно второму закону Ньютона,
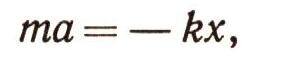
или

Если обозначить
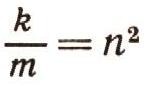
то решение уравнения (18) можно представить в виде:

где х0 есть максимальное отклонение груза (ОМ0) от положения равновесия. Предположим, что в начале движения (при t = 0) х = x0, а начальная скорость была равна нулю. Величина x0 называется амплитудой колебаний, a (nt) - фазой колебаний. Движение, определяемое законом (19), будет периодическим. В самом деле функция f(t) называется периодической, с периодом Т, если, прибавляя Т к аргументу функции, мы не изменяем ее значения, т. е.
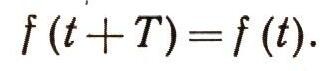
В нашем случае из уравнения (19) имеем:
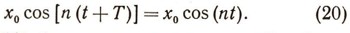
Равенство (20) будет иметь место, если пТ = 2Пи и, следовательно,
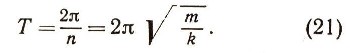
Формула (21) показывает, что период гармонических колебаний не зависит от амплитуды х0, а определяется массой колеблющегося груза и коэффициентом жесткости k. Таким образом, будет ли амплитуда колебаний х0 или 1/2х0, период будет тот же самый. Это свойство гармонических колебаний называется изохронностью, т. е. равновременностью колебаний. Свойством изохронности обладают малые колебания математического маятника. Математический маятник можно осуществить на практике в виде достаточно тяжелого шарика, подвешенного на гибкой нерастяжимой нити. Масса нити должна быть малой по сравнению с массой шарика.
Рассмотрим случай малых колебаний математического маятника, когда угол фmах мал (рис. 9).
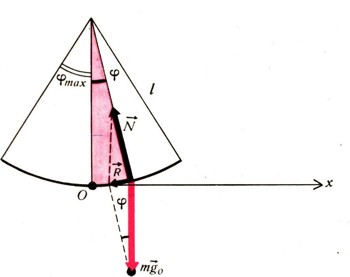
Если рассмотреть какое-то промежуточное положение маятника, то с высокой степенью точности равнодействующая сила тяжести mg0 и натяжения нити N, равная R, будет по величине равна
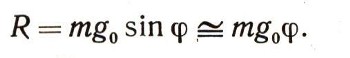
Из второго закона Ньютона мы получим:

или
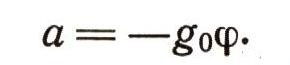
Умножая правую и левую части (22) на длину маятника l и замечая, что для малых ф,
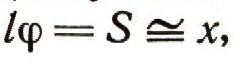
получим:

Уравнение (23) совпадает с (18), если
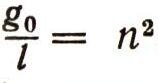
Следовательно, период малых колебаний математического маятника определится по формуле
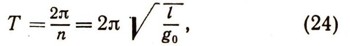
где l — длина маятника.
Таким образом, малые колебания математического маятника обладают свойством изохронности, и такой маятник можно применять для измерения промежутков времени. Это свойство малых колебаний открыл Г. Галилей.
Вот как рассказывает об этом академик А. Н. Крылов в книге "Вибрация судов": "Триста пятьдесят лет тому назад Галилей в Флорентийском кафедральном соборе, видимо, с гораздо большим вниманием следил за качаниями паникадила, нежели слушал мессу и проповедь архиерея. Паникадило, висевшее из высокого купола собора, совершало раз-махи медленно, примерно в 7 секунд, справа налево, так что Галилею было легко вести двойной счет числа размахов и биений своего пульса. Месса была длинная; размахи паникадила становились все меньше и меньше, а между тем продолжительность каждого размаха оставалась неизменной. Так по преданию Галилей открыл свойство изохронности малых колебаний маятника".
Если период колебаний маятника известен, то из уравнения (22) мы можем определить ускорение свободного падения в данной области пространства:
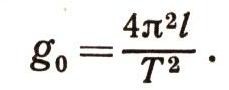
2i.SU ©® 2015