Прямолинейное движение

Пользуясь вторым законом Ньютона, исследуем простейшие случаи прямолинейного движения материальной точки. Бели равнодействующая приложенных к точке сил равна нулю, то точка будет находиться в состоянии покоя, или равномерного прямолинейного движения:

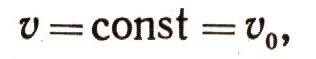
где v₀ — скорость точки в начальный момент времени (при t = 0). Если по оси абсцисс откладывать время t, а по оси ординат скорость, то легко понять, что графиком скорости будет прямая, параллельная оси времени (рис. 4). Элементарный отрезок пути

Рис. 4. График скорости (`v=v₀).

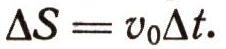
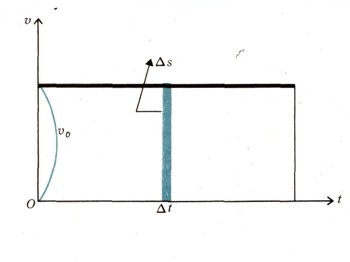
Путь за время t можно найти суммированием дельта S. Следовательно,

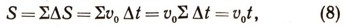
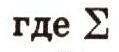
- знак суммирования. Рассмотрим случай равнопеременного (равноускоренного или равнозамедленного) движения или движения с постоянным ускорением (случай, когда ускорение точки

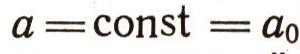
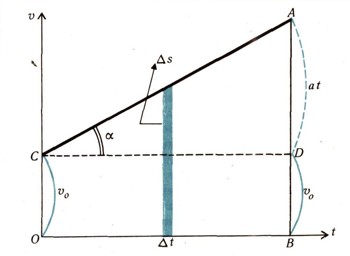
График ускорения будет изображаться прямой, параллельной оси абсцисс (рис. 5). Элементарное приращение скорости за время дельта t будет

Рис. 5. График ускорения (а=a₀).

Рис. 6.

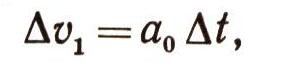
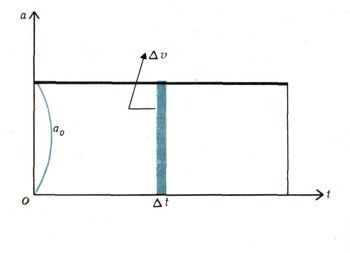
а следовательно,

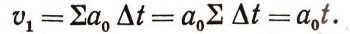
Если в начале движения (при t = 0) точка имела скорость v₀, то полная скорость будет равна сумме v₀ + v₁ т. е.

График скорости (для определенности — равноускоренного движения, т. е. для а₀ > 0) будет представлять прямую линию, наклоненную к оси абсцисс под углом, тангенс которого равен a₀(tg a = а₀). Элементарный путь дельта S будет подсчитываться по формуле

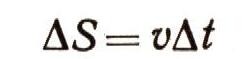
и будет изображаться на рисунке в голубым столбиком. Пройденный точкой путь

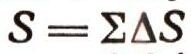
будет представлять собой площадь трапеции ОСАВ. Эту площадь можно вычислить, прибавляя к площади прямоугольника OCDB площадь треугольника CAD. Следовательно,

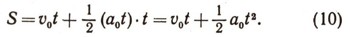
Весьма полезная формула для вычисления пути S получится, если мы воспользуемся общеизвестной формулой для площади трапеции:

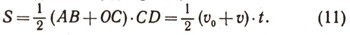
Для дальнейшего полезно ввести понятие работы силы. Так как мы рассматриваем только прямолинейные движения, то для этих случаев элементарную работу определяют как произведение силы на элементарное перемещение. Если направление силы совпадает с направлением элементарного перемещения, то элементарная работа будет положительной; если направления элементарного перемещения и силы противоположны, то работа будет отрицательной. Работа силы на конечном участке пути находится суммированием элементарных работ. Если сила постоянна, то суммирование элементарных работ легко провести. Подсчитаем работу силы тяжести Р = mg₀ при падении тела (точки) с высоты А (рис. 7). Элементарная работа будет

Рис. 7.

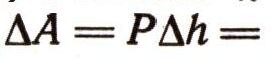
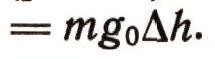
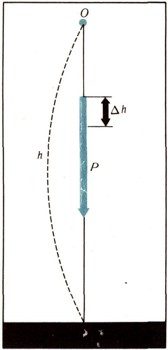
Работа силы Р на пути h определится так:

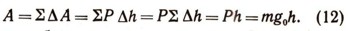
Таким образом, при падении тела (точки) с постоянной массой под действием силы тяжести работа равна произведению этой силы на высоту, с которой тело падало. Рассмотрим закономерности движения в однородном поле силы тяжести. В этом случае действующая сила будет Р = mg₀ = const. Из второго закона Ньютона следует, что движение точки будет равноускоренным с ускорением a = g₀ = const.

Пусть материальная точка массы т начинает падать из точки O,, расположенной на высоте h₀, имея при этом начальную скорость, равную v₀; на высоте h₁<h₀ скорость точки будет v₁Определим зависимость между v₀ и v₁. Пользуясь формулами равноускоренного движения, имеем:

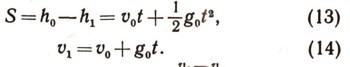
Из формулы (14) определим

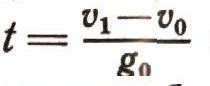
и подставим в формулу (13). После простых преобразований получим :

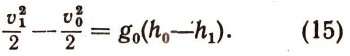
Умножим правую и левую части соотношения (15) на массу точки т:

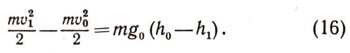
Величина, равная половине произведения массы точки на квадрат ее скорости, называется кинетической энергией точки. Формула (16) представляет один частный случай теоремы об изменении кинетической энергии. Полученный результат можно сформулировать так: изменение кинетической энергии материальной точки, движущейся в однородном поле силы тяжести, равняется работе силы тяжести на пройденном пути: S = h₀ - h₁. Формулу (16) можно переписать в виде:

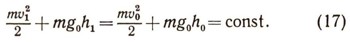
Величину Ph₁ = mg₀h₁ называют потенциальной энергией материальной точки на высоте h₁ и соответственно Ph₀ = mg₀h₀ - потенциальной энергией на высоте h₀.

Формула (17) утверждает, что при движении материальной точки в однородном поле силы тяжести сумма кинетической и потенциальной энергий точки есть величина постоянная. Это закон сохранения механической энергии точки. Закон сохранения механической энергии справедлив и для некоторых переменных сил, например для гравитационной силы, изменяющейся обратно пропорционально квадрату расстояния до притягивающего центра, а также для силы упругости, подчиняющейся закону Гука (сила прямо пропорциональна отклонению от положения равновесия).

перейти к началу страницы