Закон параллелограмма сил

Изучаемые в механике физические величины можно разделить на два класса: скалярные и векторные. Скалярные величины полностью характеризуются их численным значением. К таким величинам можно, например, отнести площадь, объем, плотность и др. Векторные величины характеризуются не только их значением, но и направлением в пространстве.

Сила и скорость - величины векторные. Графически векторные величины изображаются стрелкой. Длина отрезка при выбранном масштабе дает величину (модуль) вектора, стрелка показывает направление действия вектора.

Рис. 1.

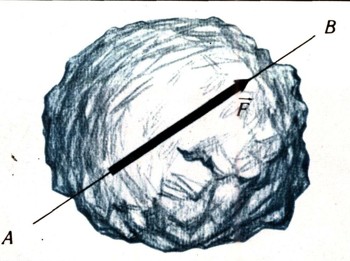
На рисунке 1 изображен вектор силы. Векторы обозначают латинскими буквами со стрелкой наверху. Так, на рисунке 2 буквами F₁,F₂,F₃ показаны три силы, действующие на тело так, что их точки приложения совпадают. Те же буквы без стрелок обозначают численные значения сил.

Рис. 2.

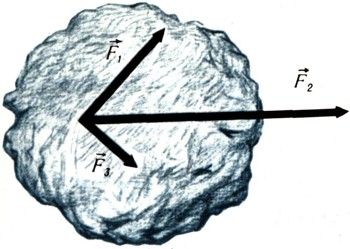
Важнейшим законом, которому подчиняются силы, является закон независимого действия сил. Этот закон основывается на многочисленных опытах, и его можно формулировать так: действие каждой из приложенных к телу сил (например, F₁ F₂, F₃)

не зависит от того, находится это тело в покое или в движении, и не зависит от числа действующих сил. Действие любой силы данной системы сил не зависит от действия других сил.

Рис. 3.

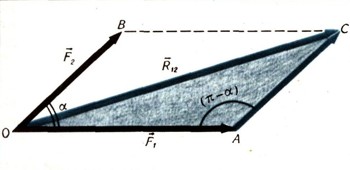
Следствием закона независимого действия сил является правило сложения двух сил. По существу это правило сложения векторов. Чтобы сложить два вектора, выбирают подходящий масштаб и вычерчивают их в этом масштабе из одной точки, а затем строят на складываемых векторах параллелограмм (рис. 3). Тогда сумма векторов будет изображаться диагональю параллелограмма, соединяющей исходную точку с противоположной вершиной. Векторную сумму сил F₁ и F₂ называют равнодействующей этих сил. Математически векторное сложение сил F₁ и F₂ можно записать так:

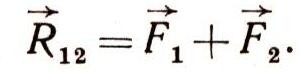
Если угол между F₁ и F₂ обозначить а, то по теореме косинусов из треугольника ОАC мы легко найдем значение равнодействующей:

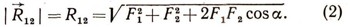
В частном случае, когда а = 0 (силы направлены по одной прямой в одну сторону),

Если

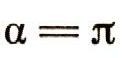
(силы направлены по одной прямой в разные стороны), тогда

перейти к началу страницы