Картографические проекции

С тех пор ученые создали много различных способов приближенного изображения поверхности земного шара на картах, или картографических проекций, в основе которых лежат разные способы построения географической сетки.

Рассматривая глобус, не трудно убедиться, что все меридианы представляют собой большие (на глобусе они все одинаковой длины) окружности, пересекающиеся между собой только в двух точках — полюсах. Зато каждый меридиан пересекает все параллели, т. е. окружности, проведенные к ним под прямым углом. Самая длинная из окружностей-параллелей — это экватор, все точки которого отстоят от полюсов на равных расстояниях. С приближением к полюсам длина параллелей уменьшается, в пределе, сливаясь в одну точку. На картах же, в зависимости от выбранной проекции, меридианы и параллели изображаются то прямыми, а то различными кривыми линиями. Выбор проекции зависит от назначения карты. Например, для составления политической карты Европы более подходит такая проекция, которая дает правильное представление о размерах территории государств, позволяет сравнивать их площади. Проекции, при которых все площади одинаково уменьшаются, т. е. их отношения не искажаются, называются равновеликими. Напротив, для целей навигации (вождения кораблей и самолетов) нужны карты в равноугольных проекциях, на которых углы между различными направлениями на земной поверхности изображаются в натуральную величину, хотя при этом не сохраняются соотношения площадей.

Способы построения картографических проекций

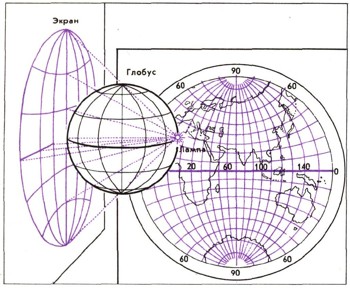
Схема построения азимутальной экваториальной проекции и карта Восточного полушария в этой же проекции.

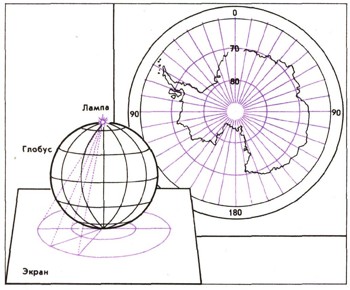
Схема построения азимутальной полярной проекции и карта Антарктиды в этой же проекции.

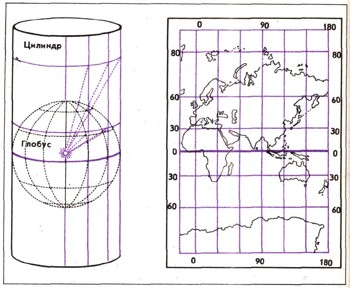
Схема построения цилиндрической проекции. Жирная линия —'линия касания шара цилиндром. Справа — карта Восточного полушария в меркаторской проекции.

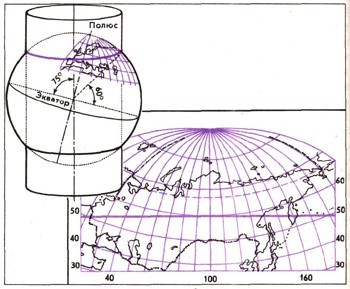
Положение глобуса и секущего цилиндра, на котором строится проекция М. Д. Соловьева. Жирная линия показывает линию пересечения шара цилиндром. По этой линии сохраняется точный масштаб. Справа — карта СССР в проекции М. Д. Соловьева.

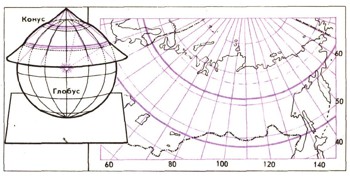
Схема конической проекции на секущем конусе. Жирными линиями обозначены параллели сечения шара конусом. На этих параллелях сохраняется точный масштаб. Справа — карта СССР в конической равнопромежуточной проекции В. В. Каврайского.

Чтобы яснее представить себе приемы построения равноугольной проекции, вообразим, что мы взяли глобус, сделанный из прозрачного материала, и экран из прозрачной бумаги прислонили к одной из точек экватора. Если теперь осветить с другой стороны глобус лампой, расположенной на уровне экватора, на экран будет падать тень от изображенных на глобусе меридианов и параллелей, а также от очертаний континентов, морей и т. п. Обведя спроектированное на плоскую поверхность экрана изображение, мы получим карту в так называемой азимутальной экваториальной проекции, которая обычно применяется для изображения полушарий.

Если приложить экран к точке полюса глобуса, а лампу держать против другого полюса, то спроектируется карта в азимутальной полярной проекции. Она дает представление о приполярных областях.

Если же надеть на глобус цилиндр из прозрачной бумаги так, чтобы он касался линии экватора, а лампочку поместить внутри глобуса, на поверхности цилиндра получим изображение в цилиндрической проекции. .

Развернув поверхность цилиндра, мы увидим, что меридианы и параллели превратились в пересекающиеся под прямыми углами параллельные линии. В этой проекции искажения увеличиваются по мере удаления от экватора к полюсам, и ее следует применять для изображения стран, расположенных вблизи экватора.

Особенно велики искажения расстояний и площадей на цилиндрической проекции голландского картографа Меркатора. В полярных странах они так преувеличены, что площадь изображения Гренландии больше, чем всей Южной Америки, которая превосходит ее в действительности в восемь раз, а расстояние от Кольского полуострова до Чукотки кажется таким же, как от Кубы до Цейлона, хотя второе в два раза больше. Зато на этой карте легко определять нужное направление, т. е. углы-румбы, а это крайне важно в мореплавании и в авиации.

Чтобы проложить на карте путь корабля или самолета, штурман должен точно определить и направление движения, и протяженность каждого участка маршрута. Линия, пересекающая все меридианы под одним и тем же углом, называется локсодромией (по-гречески «локос» — косой, «дромос» — путь). На меркаторской карте она выглядит прямой линией: измерил угол транспортиром и держи курс по компасу. Но кратчайшее расстояние между двумя точками на сфере определяется по ортодромии (по-гречески «ортос» — прямой), которая пересекает меридианы под разными углами.

Широко распространены конические проекции, применяемые для изображения стран, лежащих в средних широтах и вытянутых с запада на восток, например для СССР. На картах в этой проекции меридианы изображаются прямыми линиями, расходящимися веером из одной точки, а параллели — дугами кругов с центром в той же точке полюса. Чтобы получить такую проекцию, наденем на наш прозрачный глобус бумажный конус так, чтобы он касался его по одной из параллелей. Если теперь осветить глобус с противоположной стороны и спроектировать его на поверхность конуса, а затем конус развернуть, то мы и получим карту в виде сектора. Точный масштаб на ней сохраняется по параллели, по которой конус касался глобуса; по мере удаления от нее искажения возрастают. Чтобы уменьшить эти искажения, используют не касательный, а секущий конус — тогда точный масштаб сохраняется по двум параллелям. Расчетом таких проекций занимается математическая картография.

Конечно, вид полушария, развернутого цилиндра или сектора имеет карта, на которой спроектирован весь земной шар. Обычно же на карте изображается лишь часть земной поверхности, как бы вырезанная из полушария, цилиндра или сектора. При этом рамки географической карты могут быть произвольными, а на топографических они совпадают с меридианами и параллелями.

перейти к началу страницы