Астрономия

Содержание раздела

Изучение Вселенной при помощи космонавтики

Законы движения искусственных небесных тел

Физика и астрономия указали на принципиальную возможность выхода человека в космос при помощи искусственных небесных тел, посылаемых с Земли с огромными скоростями.

Принцип технической возможности развить огромные скорости, необходимые для запуска искусственных небесных тел, - принцип ракетного движения - был разработан нашим великим соотечественником К. Э. Циолковским (1857-1935).

В конце XVII в. Ньютон сформулировал закон всемирного тяготения - основной закон, которому подчиняется движение всех небесных тел. В свободном орбитальном полете, т. е. в полете по своей орбите без двигателей, космические ракеты и спутники, т. е. искусственные небесные тела, полностью подчиняются законам небесной механики. (Раздел астрономии, изучающий весь комплекс законов движения небесных тел, называется небесной механикой. О ней рассказывается в статье "Закон всемирного тяготения". О реактивном движении и о технике космических полетов будет рассказано в томах 3 и 5 ДЭ.) Поэтому теория движения искусственных небесных тел целиком опирается на результаты изучения движения небесных тел вообще.

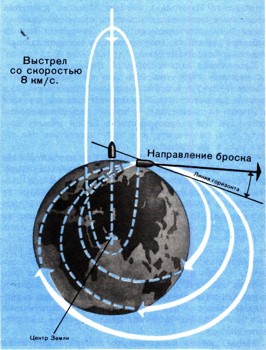
Всем нам по опыту известно, как ведет себя брошенный камень - он падает на Землю под действием притяжения Земли. Ну а если не бросать камень, а выстрелить из пушки вертикально вверх? Когда вся энергия, полученная снарядом при выстреле, будет израсходована на преодоление земного тяготения, снаряд остановится и начнет падать обратно. Законы "бросания" тел изучает баллистика. Одна из основных задач баллистики заключается в том, чтобы найти такой угол наклона ствола орудия, при котором, при прочих равных условиях, дальность выброшенного орудием снаряда будет наибольшей. Но можно сделать и так, что снаряд не упадет на Землю. Давайте проследим за полетом снаряда, выброшенного из орудия, ствол которого расположен наклонно к линии горизонта.

Небесная механика утверждает, что под действием сил тяготения одно тело описывает относительно другого одну из трех кривых - эллипс, параболу или гиперболу. Так, например, все планеты обращаются вокруг Солнца по эллипсам, причем само Солнце располагается в одном из фокусов эллиптической орбиты планеты. Так же и в системе "Земля - снаряд" центр Земли будет всегда в одном из фокусов эллипса, по которому движется снаряд. Поэтому если выстрелить наклонно, то чем больше будет увеличиваться скорость, тем все дальше и дальше будет падать снаряд. Чем больше будет его скорость (до некоторого предела), тем больший эллипс он опишет в пространстве, но на обратном пути к точке бросания он обязательно должен пройти "сквозь Землю", так как может двигаться только по эллиптической траектории, часть которой всегда проходит внутри Земли.

Итак, при наклонном выстреле снаряд в любом случае должен упасть на Землю. Попробуем теперь установить наше орудие на горе и стрелять горизонтально (для простоты мы не будем учитывать сопротивление земной атмосферы и вращение Земли). При небольших скоростях снаряды, двигаясь по эллипсу, будут падать на Землю. Но чем больше начальная скорость снаряда, тем больше эллипс будет приближаться к окружности с центром в центре Земли. При скорости, которую принято называть первой космической или круговой, снаряд уже не упадет на Землю, а, если мы успеем убрать орудие, пролетит с той же скоростью через точку выстрела и будет бесконечно обращаться вокруг Земли по круговой орбите, т. е. станет искусственным спутником Земли.

Первая космическая скорость у поверхности Земли составляет примерно 7,9 км/с. Такую огромную скорость не может сообщить снаряду ни одна пушка - это под силу только ракетам, как было доказано К. Э. Циолковским. Он явился основоположником теории полетов за пределами Земли.

Дальнейшее увеличение скорости будет вытягивать окружность в эллипсы, с той только разницей, что второй фокус каждого эллипса будет перемещаться все дальше и дальше от центра Земли в сторону, противоположную направлению бросания. Современные ракеты сообщают космическим аппаратам нужные начальные скорости движения.

При скорости 11 км/с тело удалится на расстояние больше половины расстояния до Луны, а при скорости 11,1 км/с тело залетит за орбиту Луны и снова вернется к Земле. При дальнейшем увеличении скорости до 11,2 км/с эллиптическая орбита "разорвется" и превратится в разомкнутую кривую - параболу, по которой космический аппарат навсегда покинет Землю. Скорость 11,2 км/с называется второй космической скоростью, или параболической, или скоростью отрыва.

Космический аппарат, получивший такую скорость на поверхности Земли, покинет ее навсегда как при вертикальном, так и при наклонном или горизонтальном полете. При такой скорости в любом случае орбита не будет эллипсом. Если еще больше увеличить скорость, космический аппарат полетит уже по кривой, называемой гиперболой, причем чем выше скорость, тем шире будет "раскрываться" гипербола. Но, превысив вторую космическую скорость и преодолев земное притяжение, космический аппарат все же останется в Солнечной системе. Он превратится в спутника Солнца - искусственную планету - и будет обращаться вокруг него по эллиптической орбите.

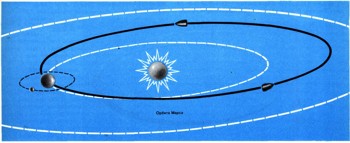
Первым таким спутником Солнца стала советская космическая ракета "Луна-1", стартовавшая 2 января 1959 г. по направлению к Луне. Аппарат удалялся от Земли по гиперболической орбите. Через 5-6 сут он вышел из зоны действия земного притяжения, и его полет всецело стал определяться притяжением Солнца. Скорость, которую имел аппарат, была недостаточной, чтобы преодолеть притяжение Солнца, и он стал обращаться вокруг Солнца по эллипсу. Его вытянутая орбита располагается между орбитами Земли и Марса. Какие же основные закономерности характеризуют движение тел по эллиптическим орбитам? Ответ на этот вопрос также дает небесная механика.

Наблюдения астрономов за движением планет дали возможность немецкому ученому Кеплеру в начале XVII в. сформулировать три закона движения тел в Солнечной системе (см. ст. "От Коперника до Ньютона"). Законы Кеплера являются следствием более общего закона природы - закона всемирного тяготения, который составляет основу небесной механики. Они позволяют полностью определить орбиту планеты.

Простейшая задача небесной механики называется задачей двух тел. Что же требуется решить в этой задаче? А вот что. Если известны массы двух тел, их скорости в какой-то момент времени, а также взаимное расположение, то нужно найти положение этих двух тел в пространстве в любой момент времени, т. е. рассчитать, как будут двигаться два таких тела в пространстве.

Ньютон решил эту задачу. Он математически доказал, что если любое тело (не обязательно Солнце) считать неподвижным, то другое тело под действием их взаимного тяготения, в зависимости от начальных условий задачи (масс, скоростей и расположения), будет двигаться относительно его по эллипсу (или окружности), параболе или гиперболе. В Солнечной системе, например, взаимное притяжение планет ничтожно мало по сравнению с притяжением их Солнцем, поэтому можно считать, конечно только приблизительно, что любое тело Солнечной системы притягивается только Солнцем и движется по эллипсу. Небольшие отклонения в движении планет от движения, точно соответствующего законам Кеплера, конечно, есть, но учесть их чрезвычайно трудно.

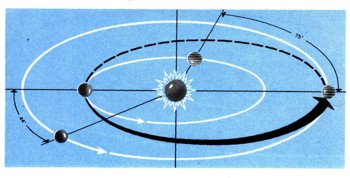
Масса любого космического аппарата ничтожно мала по сравнению с массой Земли и Луны (или Солнца). И это позволяет произвести достаточно точный расчет его орбиты. Как выглядят такие орбиты, можно представить себе на примерах трасс полетов в район нашего спутника. Посланный в район Луны космический аппарат притянется ею, обогнет ее и снова вернется к Земле, описав в пространстве замысловатую восьмерку. Для такой траектории необходимо, чтобы, во-первых, космический аппарат прошел на определенном, достаточно близком расстоянии от Луны и, во-вторых, в момент сближения с Луной обладал вполне определенной, сравнительно малой скоростью. Но если пролетать мимо планеты, например Марса или Венеры, на "почтительном" расстоянии, где сила притяжения планеты сказывается незначительно, то орбиты относительно Солнца будут представлять собой эллипсы, размеры которых определяются скоростью при взлете с Земли.

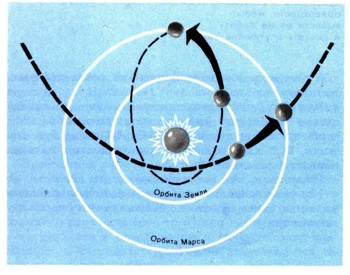
Для полета на Марс, как и на любую другую планету, наиболее выгодной и простой является эллиптическая траектория, касательная к орбите планеты. В этом случае скорость отлета с Земли минимальна (11,6 км/с), минимальна и скорость, с которой ракета подойдет к Марсу (5,7 км/с). Последнее немаловажно в случае посадки на Марс, так как меньше будет израсходовано топлива для торможония двигателями ракеты. Но за экономию топлива приходится платить временем. Такой полет будет длиться 259 сут, т. е. 8,5 мес. Если сократить срок полета до 5 мес, то необходимо будет развить скорость отлета с Земли до 14,3 км/с, а при 4 мес полета начальная скорость должна составлять 15,9 км/с. По кратчайшей траектории полет к Марсу продлился бы 85 сут, но вначале разогнать корабль нужно было бы до скорости 39 км/с.

Первые полеты космонавтов скорее всего пройдут по другим траекториям, ведь нужно не только достичь района Марса, но и вернуться обратно на Землю. Облетев планету по наивыгоднейшей траектории и возвратившись к точке старта, космический корабль не застанет Землю на том же месте - она уйдет на значительное расстояние по своей орбите. При достаточном запасе горючего и ресурсов для жизнеобеспечения при полете к Марсу можно дождаться благоприятного времени для обратного старта на самой планете или на околомарсианских орбитах. Но существуют и простейшие облетные траектории, при которых космический корабль "на обратном пути" сблизится с Землей за сравнительно небольшое время. Можно облететь Марс за 2 года. Для этого потребуется начальная скорость 12,3 км/с. Если же увеличить скорость еще на 3,9 км/с, то можно сократить срок облета до одного года.

Трудно предугадать, какой вариант будет выбран при первом полете человека к Марсу. Будет ли это просто пассивная облетная траектория, полет по наивыгоднейшей траектории с "ожиданием" на орбите около Марса (или на самом Марсе) и возвращение опять по наивыгоднейшей касательной траектории, либо полет по наивыгоднейшей траектории "туда" и старт обратно с большим расходом топлива для сокращения общего времени полета, либо какая-нибудь другая комбинация из возможных траекторий - все будет зависеть от того, что к тому времени окажется более разумным: использовать полетную массу корабля для обеспечения жизнедеятельности экипажа в течение года-двух (а может быть, и более) и расходовать минимальное количество горючего на обратный старт и маневры у планеты либо взять на борт максимум горючего, что позволит за счет активных маневров и переходов на различные траектории сократить время полета до нескольких месяцев. Очевидно, ученые и инженеры выберут "золотую середину".

А теперь несколько примеров для любителей математики. Каждому, очевидно, интересно знать: почему нужно сообщить телу скорость именно 8 км/с, чтобы оно стало спутником Земли? Почему при скорости 11,2 км/с ракета может вырваться из оков земного тяготения? Посмотрим, как рассчитываются эти скорости.

Мы уже говорили, что основой небесной механики является закон Ньютона. Математически он выражается так:

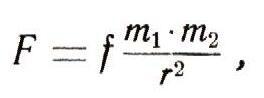
где т₁ и т₂ — массы двух тел, r — расстояние между ними, f — коэффициент пропорциональности. Для случаев, когда одно тело имеет массу т₂, пренебрежимо малую по сравнению с массой т₁ центрального тела (Земли, Солнца), принято вводить коэффициент

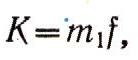
тогда

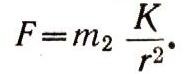
Для Земли этот коэффициент поля тяготения равен К₃ = 3,9-10⁵ км³/с², для Солнца K_C = 132,3-10⁹км³/с².  Чтобы тело стало искусственным спутником Земли и могло, не снижаясь, обращаться вокруг Земли по круговой орбите, необходимо приравнять центростремительное ускорение

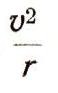
к ускорению тяготения. Тогда

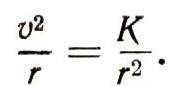
Умножив обе части равенства на r, получим:

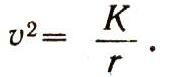
Подставив значение К, равное К₃, и радиуса Земли r=6371 км, получим величину круговой скорости, при которой тело будет удерживаться на круговой околоземной орбите:

Если мы подставим вместо К значение К_з , а вместо r расстояние от Земли до Солнца (принятое здесь за 149600000 км), то получим скорость, с которой Земля должна вращаться вокруг Солнца, чтобы удержаться на своей орбите:

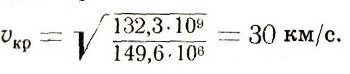
Именно с такой скоростью наша Земля движется вокруг Солнца. Первая космическая скорость, точнее ее теоретическое значение, рассчитана нами для высоты полета над Землей, равной нулю, т. е. у поверхности Земли.

При высоте полета, например, h = 500 км в формулу вместо r придется подставить r=r₀+h (где r₀ — радиус Земли). В этом случае v =7,61 км/с.
При увеличении высоты орбиты скорость движения постепенно убывает, стремясь в бесконечности к нулю. На высоте 384 тыс. км, т. е. на орбите Луны, v_кр = 1км/сЭто и есть средняя скорость движения Луны на ее орбите вокруг Земли.

Но для того чтобы запустить искусственный спутник, нужно затратить на подъем какую-то энергию и, кроме того, сообщить ему необходимую круговую скорость. Хотя круговая скорость с высотой уменьшается, энергия, затрачиваемая на подъем, растет. Поэтому общий расход энергии на подъем и разгон ракеты с высотой растет. Этот расход энергии принято характеризовать так называемой характеристической скоростью v_x. Определяется она следующей формулой:

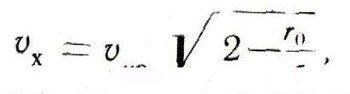
где v_кр0 - круговая скорость у поверхности Земли, r₀ - радиус Земли, r - расстояние от центра Земли до орбиты искусственного спутника Земли.

Минимальное значение v принимает при r=r₀. Тогда v_x - v_кр0 так как никаких затрат энергии на подъем не требуется. Максимальное значение v_x получается при r = бесконечности. В этом случае v_х=11,2 км/с, т. е. тело, получившее такую скорость у поверхности Земли, удалится от нее на бесконечно большое расстояние - навсегда покинет Землю. Это и есть вторая космическая скорость - скорость отрыва. Используя описанную астрономическую теорию и гениальную идею Циолковского о получении космических скоростей при помощи ракет, во второй половине нашего века люди начали изучение и освоение космоса при помощи запусков космических аппаратов.

перейти к началу страницы