Астрономия
Как развивалась наука о Вселенной
Закон всемирного тяготения
Закон всемирного тяготения отражает свойство всех материальных тел притягивать друг друга. Он был открыт в середине XVII в. великим английским ученым Ньютоном при изучении движения планет и их спутников в Солнечной системе.
Мысль о том, что небесные тела и вообще все материальные тела взаимно притягиваются, возникла еще до Ньютона. На Земле это притяжение проявляется прежде всего в существовании силы тяжести. Под действием этой силы все тела, если их ничем не поддерживать, падают вниз, точнее к центру Земли.
Работы Коперника, Кеплера, Галилея показали, что Земля - обычное небесное тело, рядовая планета, движущаяся вместе с другими планетами вокруг Солнца. Значит, другие небесные тела могут обладать теми же свойствами, что и Земля, т. е. и на них может существовать сила тяжести. Если материальные тела вблизи Земли стремятся к ее центру, то вблизи планет или Солнца они также будут стремиться к центрам этих тел. Так считали Коперник, Кеплер и другие ученые того времени. В одной из своих работ Кеплер писал: "Тяжесть есть взаимная склонность между родственными телами... соединиться воедино... В каком месте мы ни поместили бы Землю, тяжелые тела... будут двигаться к ней... Если бы в каком-нибудь месте мира находились два камня на близком расстоянии друг от друга... то эти камни стремились бы соединиться друг с другом подобно двум магнитам..."
Заслуга Ньютона состояла прежде всего в том, что он установил точную математическую зависимость сил притяжения от массы тел и от расстояния между ними и доказал, что именно эти силы "управляют движением планет и спутников в нашей Солнечной системе.
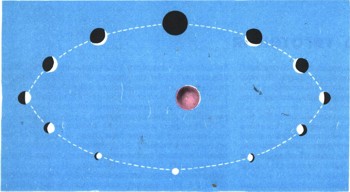
В начале XVII в. Кеплер установил основные закономерности движения планет (см. ст. "От Коперника до Ньютона"). По первому и второму законам Кеплера каждая планета движется вокруг Солнца по эллипсу, а Солнце находится в одном из фокусов этого эллипса, причем скорость движения планеты изменяется вдоль ее пути определенным образом (приближенно скорость движения планеты обратно пропорциональна ее расстоянию до Солнца). Ньютон доказал, что такая картина движения планет должна наблюдаться в том случае, если Солнце притягивает планеты с силой, обратно пропорциональной квадрату расстояния до планеты.
Во времена Ньютона были известны четыре спутника Юпитера. Наблюдения показали, что их движение подчиняется третьему закону Кеплера, т. е. квадраты их периодов обращения относятся друг к другу как кубы их расстояний от центра Юпитера. "Ньютон установил, что так должно быть именно в том случае, если спутники притягиваются к Юпитеру с силой, обратно пропорциональной квадрату расстояния до центра планеты. Вокруг Земли движется ее спутник - Луна. Ньютон доказал, что движением Луны управляет та же земная сила тяжести, но уменьшенная пропорционально квадрату расстояния Луны до центра Земли. Он рассуждал следующим образом.
Падение тел на Землю происходит с ускорением около 9,8 м/с2, другими словами, сила притяжения Земли вызывает вблизи ее поверхности, т. е. на расстоянии около 6378 км от центра, ускорение 9,8 м/с2. Среднее расстояние Луны от Земли около 384 000 км. На таком расстоянии сила притяжения Землей уменьшится в (384 000)2:(6378)2~3640 раз и ускорение будет равным 9,8/3640 ~ 0,0027 м/с2. Но именно таким центростремительным ускорением обладает Луна, движущаяся примерно по окружности вокруг Земли. Следовательно, Луна движется под действием силы земного притяжения.
На основании всего этого Ньютон заключил, что обращением всех планет вокруг Солнца, спутников Юпитера вокруг Юпитера, Луны вокруг Земли управляет сила, имеющая один и тот же характер. Это сила притяжения к центру того небесного тела, вокруг которого происходит движение, причем эта сила убывает пропорционально квадрату расстояния. Пропорциональная зависимость этой силы от массы вытекает из следующего соображения. Сила тяжести на Земле определяет вес тела, а вес увеличивается пропорционально массе тела. Следовательно, сила притяжения пропорциональна массе тел.
Вот таким путем Ньютон пришел к своему знаменитому закону, который был назван впоследствии законом всемирного тяготения: "Каждые две материальные частицы притягивают друг друга с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними".
Математически этот закон выражается формулой
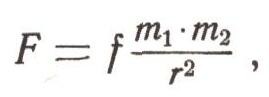
где F - сила взаимного притяжения, m1 и m2 -массы притягивающихся частиц, r - расстояние между ними. Коэффициент пропорциональности f в этой формуле одинаков для всех материальных частиц и называется постоянной тяготения.
Притяжение между большими материальными телами складывается из сил притяжения между частицами, из которых эти тела состоят. Если расстояние между телами очень велико по сравнению с их размерами, то эти тела притягивают друг друга практически так же, как и материальные частицы. Однако если рассмотреть, например, притяжение Землей какого-нибудь тела вблизи ее поверхности, то само понятие расстояния между Землей и этим телом становится неопределенным; можно говорить о расстоянии до ближайшей точки поверхности Земли, до центра Земли и т. д. Если мысленно разбить Землю на небольшие частицы с равными массами, то эти частицы будут притягивать данное тело с разными силами. Какому же закону будет подчиняться суммарное притяжение Земли, если каждая частица Земли притягивает с силой, обратно пропорциональной квадрату расстояния до нее? В этом случае результат оказывается неожиданно простым. Еще Ньютон доказал, что шарообразные тела, какими являются Земля, планеты, Солнце, притягивают почти по такому же закону, что и материальные частицы, если расстояние измерять от их центров. Но если материальные тела имеют более сложную форму и структуру, закон суммарного притяжения гораздо сложнее.
Закон всемирного тяготения предоставил новые возможности для изучения движения небесных тел. Стало возможным рассчитывать точные траектории небесных тел в пространстве на много лет вперед, восстанавливать траектории их движения в далеком прошлом. В настоящее время большое значение имеют расчеты движения искусственных спутников Земли, автоматических межпланетных станций и других искусственных небесных тел.
Действием сил притяжения объясняются многие наблюдаемые явления, например приливы и отливы на Земле (см. ст. "Приливы и отливы"). Из-за совместного действия сил притяжения между частицами, из которых состоит Земля, и сил инерции, появляющихся при вращении, Земля имеет не точно шарообразную форму, а сплюснута у полюсов.
Закон Ньютона относится ко всем материальным телам. Следовательно, на Земле эти тела должны притягиваться не только Землей, подчиняясь силе тяжести, но также должны притягиваться между собой. Такое притяжение было действительно обнаружено. В XVIII в. ученые одной французской экспедиции в Южной Америке заметили, что вблизи гор отвес отклоняется в сторону этих гор (см. рис.). Более точные измерения отклонений отвеса провел позднее в Шотландии английский ученый Маскелайн (1732-1811).
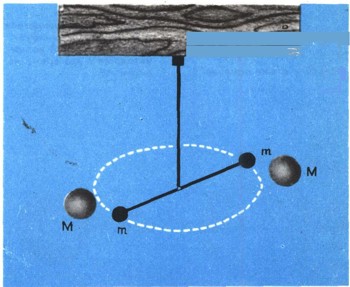
Один из лабораторных опытов по измерению силы притяжения состоит в следующем. На тонкой упругой нити подвешен горизонтально стержень с небольшими металлическими шариками массой т на концах (см. рис.). Если поднести к маленьким шарикам с разных сторон тяжелые свинцовые шары массой М, то маленькие шарики будут притягиваться к большим, весь стержень повернется и нить закрутится. По величине закручивания нити определяется действующая сила притяжения.

При таком опыте можно также, сравнивая силу притяжения с весом маленьких шариков, вычислить, во сколько раз Земля притягивает сильнее, чем большие шары, т. е. во сколько раз масса Земли больше массы больших шаров. Таким путем английский ученый Кавендиш (1731-1810) определил в 1798 г., что масса Земли равна приблизительно 6*1021 т. Значение постоянной тяготения, найденное из этих и других опытов по непосредственному измерению сил притяжения, равно 6,673-10-11Н*м2/кг2.
Зная постоянную тяготения, мы можем вычислить силу притяжения между теми или иными телами. Например, два шара массой по 1 кг притягивают друг друга на расстоянии 10 см с силой около 7 мкН. Такая сила, конечно, мала и в повседневной жизни незаметна. Однако между крупными небесными телами действуют колоссальные силы притяжения, величину которых трудно даже представить. Например, Земля притягивает Луну с силой около 2 * 1023Н.
Сила тяготения обладает очень интересными, необычными свойствами. Для нее не существует никаких преград. Она действует между телами, разделенными безвоздушным пространством и находящимися как угодно далеко друг от друга. Тяготение не поглощается межзвездной средой, не ослабевает, когда на его пути встречаются какие-либо тела. Например, в моменты лунных затмений между Солнцем и Луной находится Земля, которая могла бы преградить путь силе тяготения между Солнцем и Луной так же, как лучам света. Это повлияло бы на движение Луны. Однако такое влияние не обнаруживается.
Существование этой удивительной всепроницаю-щей силы, действующей на
любом расстоянии, находит объяснение в общей теории относительности, созданной
великим ученым нашего века Альбертом Эйнштейном (1879-1955).